NUMERICAL
ANALYSIS
WEEK 8 2004
INTEGRAL
AND
DERIVATIVE
PROBLEM
1
Calculate
integral of y=f(x)=1/(1
+ x2)
function between limits –1 ile 1 with
3 points Gauss-Legendre integration
Formula
Note: Required
roots and
coefficients :
|
coefficients |
Roots |
|
c0 0.555555555555553 |
x0 0.774596669241483
|
|
c1 0.888888888888889 |
x1 0.000000000000000 |
|
c2
0.555555555555553 |
x2 0.774596669241483 |
PROBLEM 2
PROBLEM
3
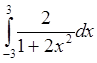solve
with bole rule.
Use n=2
Note:
Bole rule for
n=1
I=(b-a)*[7*f(x0)+32*f(x1)+12*f(x2)+32*f(x3)+7*f(x4)]/90
Step
size h=(b-a)/n
PROBLEM
4
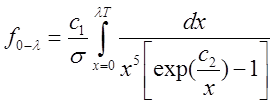
Function
is known as black
body radiation shape function.
The values
of coefficients in the equation
are:
c1
=3.743 x108
W.mm4/m2,
c2
=1.4387x104 mm.K,
s=5.67x10-8
W/(m2.K4)
dür.
Use
Gauss-Legendre integration and
for a giving
lT
calculate black
body radiation shape factor.
Create
a table for
the values
of blackbody
radiation shape
factor from
5000 to infinity(?)
PROBLEM
5
Solve the integration
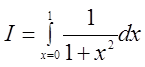
a) by analithical
methods
b) by Trapezoidal
rule with
n=2(divide region
into
2 parts) and
calculate % error
c) Trapezoidal
rule
with n=2(divide
region into
2 parts)
and calculate
% error
PROBLEM 6
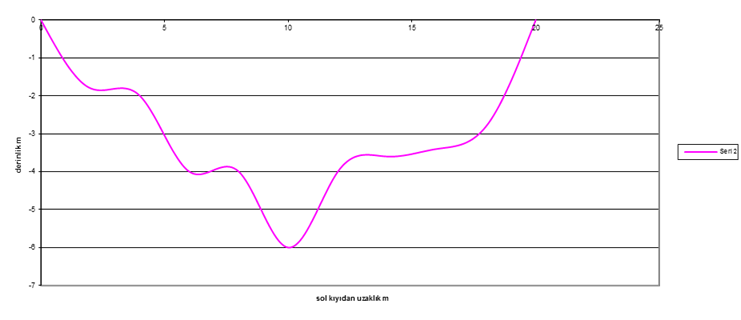
Depth(H) and velocity(U)
profile of a channel
is given in below
table
|
x,
m |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
H,
m |
0 |
1.8 |
2 |
4 |
4 |
6 |
4 |
3.6 |
3.4 |
2.8 |
0 |
|
U
m/s |
0 |
0.03 |
0.045 |
0.055 |
0.065 |
0.12 |
0.07 |
0.06 |
0.05 |
0.04 |
0 |
Cross sectiaonal area
of the channel
can be calculated as :
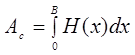
Flow rate of the channel
will be
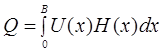In
this equations
U is the velocity
of the water
measured
at point x. Calculate
cross sectional
area and
flow
rate of the channel.
PROBLEM 7
Temperature profle of a solid
body can be given as
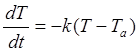
In this equation
T is the temperature,
Ta
is constant surface
temperature.
A solid
body with
temperatures initially
at T=90
C and, Ta
=20 C put into a water container
at temperature of Ta = 20 C.
The
temperature profile as a function
of time is given at the table.
|
Zaman , t,
s |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
|
Sicaklik
T C |
90 |
55 |
40 |
28 |
24 |
22 |
21.5 |
20.6 |
Calculate k thermal conductivity
coefficient.