NUMERICAL
ANALYSIS WEEK 4 2015
OPTIMISATION
PROBLEM1
An antibiotic producing
microorganism has a specific growth
rate(g) is function of food concentration
(c)
If g =
2*c/(4+0.8c+c2+0.2c3)
Find the c that will
give te maximum
growth rate. In
low food
concentrations growth rate drops
to zero,
similarly in very
high food
concentrations growth rate will
drop to
zero due
to food
poisining effect.
Because of this
reason, values
bigger than c = 10
mg/L should not be investigated.
PROBLEM
2
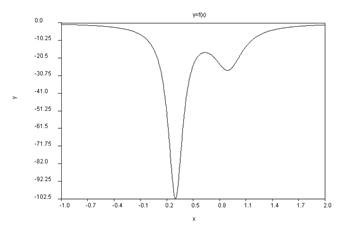
Find minimum of the function
f(x)=-(1.0/((x-0.3)*(x-0.3)+0.01)+1.0/((x-0.9)*(x-0.9)+0.04))
PROBLEM
3
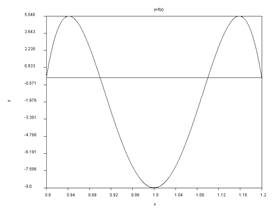
Function below is given
f(x)
= 2500x6-15000x5+14875x4+40500x3-97124x2+73248x-19008
find the minimum between x0=0.8, x1=1.2 values.
PROBLEM
4
Find the minimum of function
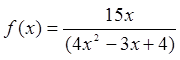find the
range of 0 to10.
PROBLEM
5
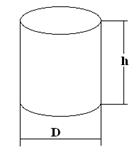
One of
the very
basic optimization
problem is the minimum cost of container
problem. The cost of a box
usually is a function
of the surface
area. Therefore
we should
minimize the area for
a given volume
For example
if the
volume of the
container
V=0.5 liter=0.5x10-3 m3 :
Volume 
or from this equation
h, height is obtained as 
.
Surface area of the cylinder
: 
.
Analytical solution of the minimization
problem
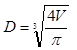. From here solution
is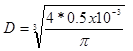 
=0.086025401 m and .
= 0.086025401 m.
Now obtain this
result by
using numerical
optimization methods.
For the range
of 0.01<=D<=0.2
a)
Graphic method
b)
Golden ratio (Fibonnachi
)
c)
Newton-Raphson root
finding
d)
Bisection root finding
method