NUMERICAL
ANALYSIS WEEK 5 2015
OPTIMISATION
PROBLEM
1
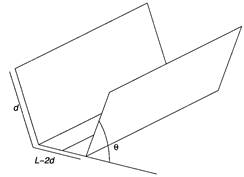
In order to construct
water channel
in a house , a flat
sheet will
be banded as shown in the
figure. Water
carrying capacity
of the channel
can be written as
V(d,q) = Z(d2sinq cosq + (L-2d)dsinq)
In this equation z is the
length of the
sheet (sheet
area is zL).
Find the
d and q to maximize water holding capacity
of the channel.
PROBLEM
2
Function below is given
f(x0, x1, x2, x3)
= (x0+10 x1)2 +5(x2-10
x3)2+(x1-2 x2)4+10(x1-
x4)4
find the minimum starting from
P(1,-1,0,1)
PROBLEM
3
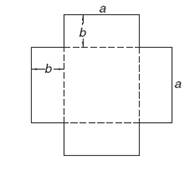
In order to
make a cartoon
box, the
shape above
should be used.After bending from
the dotted
linet he volume of the box will be 1 m3. In order
to spent
the minimum amount
of the cartoon,
what a and
b dimensions should be?
Find the minimum of
![]() .
.
PROBLEM
4
PROBLEM
5
Find the minimum of
![]()
PROBLEM
6
Non-Linear system of equations
can also be solved
by using
optimization methods
through an adaptation
function.
To solve function
fi(xj)=0
![]()
The derivative of this
equation is the
root of non-linear
system of equation
again became
fi(xj)=0, therefore optimum
of g(xj) is the same
problem as solution of fi(xj)=0.
Find the roots . Solve te following system of non-linear equations
x1(1-
x1) + 4x3 12 =0
(x1-2)2+(2x2-3)2-25
=0
By using
a)
Newton raphson method
b)
Steepest descent
optimisation method
PROBLEM
7 (Linear optimisation)
A petrochemical company
developing a new
fuel additive
for commercial
airplanes. Additive
is consist of three components
X,Y and Z. Fort
he best performance
total additive in the fuel
should be at least
6 mL/L. Due
o security reasons
the total of most
flammable X and
Y components should be less
than 3 mL/L.
Componnt X should
always be equal
or more
than the
component Y, and
componet Z should
be more than
half of the
component Y. The
cost of X,Y and
Z components are 0.15,0.025 ve 0.05 TL respectively. Find
the mixing
component tha
will give
the minimum cost.