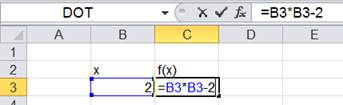
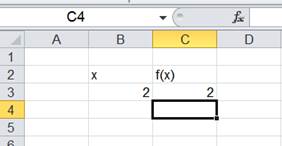
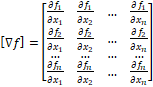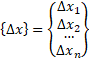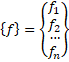COMBUSTION AND FUELS WEEK  2 (ACR)

Chemical equilibrium , Stoichiometric algorithm

 

Actual products formed in a reaction is not a clear cut concept as we defined in the previous chapter. The actual products formed in a chemical reactions can only be determined experimentally and as a function of the environmental values such as temperature, pressure and time. When these parameters changed actual products can change as well. One way of estimating what products will be formed is to use equilibrium concept. All physical systems are tend to minimize their energy levels when there are no any external force or energy to the system. For example a bubble takes spherical shape under the influence of surface tension which has the minimal area for the given volume. Chemical reactions when temperature and pressure is constant and long enough time is given, tends to minimize it energy level, specifically giibs free energy level (or maximize its entropy level). This state is called chemical equilibrium. For example consider a closed system consisting initially of a gaseous mixture of carbondioxide , oxygen and carbonic acid. A reaction might take place is 

 

At equilibrium the system will consist basically of three components, CO2, H2CO3 and H2O, for not all the components gases. This is what is called soda reaction. When soda bottle opened equailibrium condition (pressured in the system) is changed and rection slides to a new equilibrium states, so that some omount of CO2 and  H2O is formed and amount of carbonic acid is reduced .  Changes in the amounts of these components during the opening of soda bottle:

    (6.2.1)  where dn denotes the differential change in the representative component.

   (6.2.2) 

Equilibrium is a condition of balance. When equilibrium is established amount of CO2 and H2O and H2CO3 tends to be balanced with each other. But when equilibrium is broken and a new conditions arise, like opening of a soda bottle, a new equilibrium will be established. And during these process total gibbs free energy of the system will be minimised.

(6.2.3)    This amount can be determined from chemical potential changes (see the first chapter for details)

  (6.2.4)

    (6.2.5)

This is called the equilibrium reaction.For a more general equilibrium equation such as:

      (6.2.6)  where ’s are stoichiometric coefficients. The following equilibrium case is existed:

     (6.2.7)   where is the proportionality factor. From which the following expressions are obtained.

         (6.2.8) 

For this case the Gibbs free energy equation takes form:

   (6.2.9)

For ideal gas mixtures chemical potential can be expressed as specific gibbs free energy as

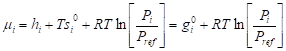    (6.2.10)   where Pi is the partial pressure of the gas. For and ideal gas, partial pressure can be expressed as a function of components in the total components

  .   (6.2.11)   Substituting these into the equation gives:

   (6.2.12)    Then the basic Gibbs free energy equation becomes

(6.2.13) 

Arranging equation:

  (6.2.14) 

  (6.2.15) 

This equation can be written as:

    (6.2.16)   or

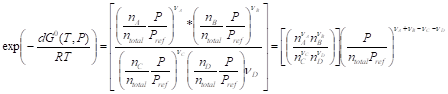  (6.2.17) 

The left hand side of the equation is called equilibrium constant, which is only function of temperature for ideal gases.

  (6.2.18) 

Equilibrium constant evaluation is already defined in chemical Reaction class. As an example let us evaluate equilibrium constant of the equilibrium reaction

 

At T=2000 K

 

chemicalReaction.java

import java.io.*;

import java.util.*;

import javax.swing.*;

import java.awt.*;

import java.awt.event.*;

 

public class chemicalReaction

{String name[];

double N[][];

Gas g[];

int natom,ngas;

int nrt,npt;

String reacName;

double A[][];

double b0[];

double b1[];

Atom atomList[];

String atomnames[];

String atomsymbols[];

chemicalReaction(String crname,String si[],double Ni[][])

{ reacName=crname;

  ngas=si.length;

name=new String[ngas];

N=new double[ngas][2];

g=new Gas[ngas];

for(int i=0;i<ngas;i++)

{  name[i]=si[i];

   g[i]=new Gas(name[i]);

}

for(int i=0;i<ngas;i++)

{N[i][0]=Ni[i][0];N[i][1]=Ni[i][1];}

     arrange_atoms();

     conservation();

}

chemicalReaction(String name) throws IOException

{ File reacFile=new File("Reaction.txt");

  int ngas;

  String tempGasName="";

  try

     {   

     BufferedReader cfin=new BufferedReader(new FileReader(reacFile));

     int ierror=1;

     natom=0;

     try

       {

       while(cfin!=null)

         {

         reacName=Text.readString(cfin);

         if(reacName.equals(name)) {ierror=0;break;}

         }

       }

       catch(EOFException e_eof)

         {

         System.out.println("error required gas mixture "+name+" is not found");

         cfin.close();return;

         }

       ngas=Text.readInt(cfin);

       g=new Gas[ngas];

       N=new double[ngas][2];

       nrt=0;

       npt=0;

 

       Double n1,n2;

       for(int i=0;i<ngas;i++)

         {

         tempGasName=Text.readString(cfin);

         N[i][0]=Text.readDouble(cfin);

         N[i][1]=Text.readDouble(cfin);

         nrt+=N[i][0];

         npt+=N[i][1];

         g[i]=new Gas(tempGasName);

         }

       }

     catch(FileNotFoundException fnfe) {System.out.println("File Not Found");}

     name=tempGasName;

     arrange_atoms();   //end of constructor

     conservation();

}    

     public void arrange_atoms()

     {

     // atomic structure of the reactants

     int i,j;

        for(i=0;i<ngas;i++)

        {for(j=0;j<g[i].natom;j++)

                 {add_atom(i,j);}

        }

     }

 

     public int  add_atom(int i,int j)

     {

     //determine and order the atomic structure

     int k;

       for(k=0;k<natom;k++)

       {

       if(g[i].atomList[j].symbol.equals(atomList[k].symbol))

         {

         atomList[k]=new Atom(atomList[k].symbol,atomList[k].N+g[i].atomList[j].N*N[i][0]);

         return 1;

         }

       }

     Atom atomL[];

     atomL=new Atom[natom+1];

     for(k=0;k<natom;k++)

       atomL[k]=new Atom(atomList[k]);

     atomL[natom]=new Atom(g[i].atomList[j].symbol,g[i].atomList[j].N*N[i][0]);

     atomList=atomL;

     natom+=1;

     return 2;

     }

     public String toString()

     {

       // writes chemical reaction in chemistry norm

       String s="";

       for(int i=0;i<ngas;i++)

       {

       if(N[i][0]==1)

           { s+=g[i].toString(); }

       else if(N[i][0]!=0)

           { s+=N[i][0]+" "+g[i].toString(); }

       if(i!=(ngas-1) && N[i][0]!=0 ) s+=" + ";

       }

       if(s.endsWith(" + "))

         s=s.substring(0,s.length()-3);

       s+=" --> ";

       for(int i=0;i<ngas;i++)

       {

       if(N[i][1]==1)

           { s+=g[i].toString(); }

       else if(N[i][1]!=0)

           { s+=N[i][1]+" "+g[i].toString(); }

       if(i!=(ngas-1) && N[i][1]!=0 ) s+=" + ";

       }

       if(s.endsWith(" + "))

         s=s.substring(0,s.length()-3);

     return s;

     }

     public String toStringE()

     {

       // writes chemical reaction in chemistry equilibrium norm

       String s="";

       for(int i=0;i<ngas;i++)

       {

       if(N[i][0]==1)

           { s+=g[i].toString(); }

       else if(N[i][0]!=0)

           { s+=N[i][0]+" "+g[i].toString(); }

       if(i!=(ngas-1) && N[i][0]!=0 ) s+=" + ";

       }

       if(s.endsWith(" + "))

         s=s.substring(0,s.length()-3);

       s+=" "+'\u21C4'+" ";

       for(int i=0;i<ngas;i++)

       {

       if(N[i][1]==1)

           { s+=g[i].toString(); }

       else if(N[i][1]!=0)

           { s+=N[i][1]+" "+g[i].toString(); }

       if(i!=(ngas-1) && N[i][1]!=0 ) s+=" + ";

       }

       if(s.endsWith(" + "))

         s=s.substring(0,s.length()-3);

     return s;

     }

     public String toString(String ch)

     {

     //return the c

     String s="";

     int i,j;

     if(ch.equals("name"))

        s=s+reacName+"\n";

     else if(ch.equals("formula"))

        {

        s=toString();

        }

     else if(ch.equals("composition"))

        {

        for(i=0;i<natom;i++)

        s=s+atomList[i].toString()+" ";

        }

     return s;

     }    

     public double H(double TR,double TP)

     {

     // reaction enthalpy

      double HH=0;

      double h1,h2;

      for(int i=0;i<ngas;i++)

      {

       h1=g[i].ht(TP)*N[i][1];

       h2=g[i].ht(TR)*N[i][0];

       //System.out.println("h1="+h1+"h2="+h2);

               HH+=h1;

       HH-=h2;

      }

      return HH;

     }

     public double S(double TR,double TP,double pt)

     {

     //reaction entropy

      double TP1,TR1,pt1;

      double s1,s2;

      TR1=TR;TP1=TP;pt1=pt;

      double SS=0;

      for(int i=0;i<ngas;i++)

      {

       if(N[i][1]!=0)

          SS+=g[i].si(TP1,N[i][1]/npt*pt1)*N[i][0];

       if(N[i][0]!=0)

          SS-=g[i].Si(TR1,N[i][0]/nrt*pt1)*N[i][1];

      }

        return SS;

     }

     public double S(double TR,double TP)

     {

     //reaction entropy

      double TP1,TR1,pt1,pt;

      pt=1.0;TR1=TR;TP1=TP;pt1=pt;

      return S(TR,TP,pt);

     }

     public double G(double TR,double TP,double pt)

     {

     // reaction gibbs energy

      double TP1,TR1,pt1;

      TR1=TR;TP1=TP;pt1=pt;

      double GG=0;

      for(int i=0;i<ngas;i++)

      {

       if(N[i][1]!=0)

          GG+=g[i].gt(TP1,N[i][1]/npt*pt1)*N[i][1];

       if(N[i][0]!=0)

          GG-=g[i].gt(TR1,N[i][0]/nrt*pt1)*N[i][0];

      }

        return GG;

     }

    

     public double G(double TR,double TP)

     { // reaction gibbs energy

       double TP1,TR1,pt1,pt;

       pt=1.0;TR1=TR;TP1=TP;pt1=pt;

       return G(TR,TP,pt);

     }

    

     public double G0(double TR,double TP)

     {

     // reaction gibbs energy

      double GG=0;

      double h1=0;

      for(int i=0;i<ngas;i++)

      {

       if(N[i][1]!=0)

          { h1=g[i].gt(TP)*N[i][1];GG+=h1;}

       if(N[i][0]!=0)

          { h1=g[i].gt(TR)*N[i][0];GG-=h1;}

      }

       return GG;

     }

     public double K(double TR,double TP)

     {

     // Equilibrium costant. Usually TR and TP will be in

     // the same temperature

     return Math.exp(G0(TR,TP)/(-8.3145*TP));

     }

     public double lnK(double TR,double TP)

     {

     // Equilibrium costant. Usually TR and TP will be in

     // the same temperature

     return G0(TR,TP)/(-8.3145*TP);

     }    

     public boolean conservation()

     {                   //Gives atomic mass balance of the chemical reaction

                 atomnames=new String[natom];

                 atomsymbols=new String[natom];

                         boolean bb=true;

                 int nn=ngas;

                                         int nat=g[0].atomList[0].atom_name.length;

                                         double B[][]=new double[nat][nn];

                                         int nk=0;                

                                         for(int i=0;i<nn;i++)

                                         {

                                                   for(nk=0;nk<g[i].atomList.length;nk++){

                                                              B[g[i].atomList[nk].number-1][i]=g[i].atomList[nk].N;

                                                           }

                                                }

                                         int natcount=0;

                                         boolean zeroflag[]=new boolean[nat];

                                         for(int j=0;j<nat;j++)

                                         {  zeroflag[j]=false;

                                            for(int i=0;i<nn;i++)

                                            {if(B[j][i]!=0){zeroflag[j]=true;}};

                                            if(zeroflag[j])

                                            {atomnames[natcount]=g[0].atomList[0].atom_name[j];

                                             atomsymbols[natcount]=g[0].atomList[0].atom_symbol[j];

                                             natcount++;}

                                         }

                                         A=new double[natcount][nn];                     

                                         int k=0;

                                         for(int j=0;j<nat;j++)

                                          {if(zeroflag[j]){A[k]=B[j];k++;}}  

                                         natom=A.length;

                                         ngas=A[0].length;

                                         b0=new double[natom];

                                         for(int ii=0;ii<natom;ii++)

                                         {

                                                  for(int ij=0;ij<ngas;ij++)

                                                  {

                                                             double carpim=A[ii][ij]*N[ij][0];       

                                                             b0[ii]+=carpim;                    

                                                  }                                                                 

                                         }

                                          b1=new double[natom];

                                         for(int ii=0;ii<natom;ii++)

                                         {

                                                  for(int ij=0;ij<ngas;ij++)

                                                     {

                                                             double carpim=A[ii][ij]*N[ij][1];       

                                                             b1[ii]+=carpim;                    

                                                     }                                                               

                                         }

                                         for(int ii=0;ii<natom;ii++)

                                                {

                    if(b0[ii]==b1[ii]) bb=bb&&true;

                    else                              bb=bb&&false;

                                                }

                                                return bb;                                               

     }

     public  void equilibrium_print(double TR,double TP)

     {

     JTextArea jta;

     JPanel jpan=new JPanel();

     jpan.setLayout(new BorderLayout());

     String s="Equilibrium Reaction name  : "+toString("name")+"\n";

     s+="Equilibrium  formula     : "+toStringE()+"\n";

     s+="Treactant = "+TR+" degree K\n";

     s+="Tproduct  = "+TP+ " degree K\n";

     s+="Equilibrium constant K = "+K(TR,TP)+"\n";

     s+="Equilibrium constant lnK = "+lnK(TR,TP)+"\n";

      s+="Equilibrium constant log10K = "+Math.log10(K(TR,TP))+"\n";

     s+="Reaction composition : "+toString("composition")+"\n";

     s+="Atom balance check   : "+conservation()+"\n";   

     s+="Atomic balance:";

     jta=new JTextArea(s);

     natom=A.length;

     ngas=A[0].length;

     String bb="Equilibrium Chemical Reaction";

     String baslik[]=new String[ngas+3];

     String s1[][]=new String[natom][ngas+3];

     int i,j;

     for(i=0;i<ngas;i++)

     {baslik[i+1]=g[i].gasName;}

     baslik[i+1]="b0(reactants)";

     baslik[i+2]="b1(products)";

    

     for(j=0;j<natom;j++)

     {s1[j][0]=atomsymbols[j];}

     for(j=0;j<natom;j++)

      { for(i=0;i<ngas;i++)

         {s1[j][i+1]=""+A[j][i];}

      }

      for(j=0;j<natom;j++)

         {s1[j][i+1]=""+b0[j];

          s1[j][i+2]=""+b1[j];

         }

             JTable jt;

             int n=A.length;

             int m=A[0].length;

             genelModel gm=new genelModel(s1,baslik);

             jt=new JTable(gm);

              //JOptionPane.showMessageDialog(null,jt);

              jpan.add(jta,BorderLayout.NORTH);

              jpan.add(new JScrollPane(jt),BorderLayout.SOUTH);

     JFrame cerceve=new JFrame(bb);

     cerceve.addWindowListener(new BasicWindowMonitor());

     cerceve.getContentPane().add(new JScrollPane(jpan));

     cerceve.pack();

     cerceve.setVisible(true);

             }

     public  void print(double TR,double TP)

     {

     JTextArea jta;

     JPanel jpan=new JPanel();

     jpan.setLayout(new BorderLayout());

     String s="Reaction name  : "+toString("name")+"\n";

     s+="Reaction formula     : "+toString("formula")+"\n";

     s+="Reaction composition : "+toString("composition")+"\n";

     s+="Atom balance check   : "+conservation()+"\n";

     s+="Treactant = "+TR+" degree K\n";

     s+="Tproduct  = "+TP+ " degree K\n";

     double Taf=Tadiabatic(TR);

     s+="Adiabatic flame temperature = "+Taf+"\n";

     double Q1=H(298.15,298.15);

     s+="Heating value = "+Q1+" kJ/kmol\n";

     double Q2=H(TR,TP);

     s+="Q = "+Q2+" kJ/kmol \n";

     s+="heating efficiency = "+Q2/Q1+"\n";

     s+="\n";

     s+="Atomic balance:";

     jta=new JTextArea(s);

     natom=A.length;

     ngas=A[0].length;

     String bb="Chemical Reaction";

     String baslik[]=new String[ngas+3];

     String s1[][]=new String[natom][ngas+3];

     int i,j;

     for(i=0;i<ngas;i++)

     {baslik[i+1]=g[i].gasName;}

     baslik[i+1]="b0(reactants)";

     baslik[i+2]="b1(products)";

    

     for(j=0;j<natom;j++)

     {s1[j][0]=atomsymbols[j];}

     for(j=0;j<natom;j++)

      { for(i=0;i<ngas;i++)

         {s1[j][i+1]=""+A[j][i];}

      }

      for(j=0;j<natom;j++)

         {s1[j][i+1]=""+b0[j];

          s1[j][i+2]=""+b1[j];

         }

             JTable jt;

             int n=A.length;

             int m=A[0].length;

             genelModel gm=new genelModel(s1,baslik);

             jt=new JTable(gm);

              //JOptionPane.showMessageDialog(null,jt);

              jpan.add(jta,BorderLayout.NORTH);

              jpan.add(new JScrollPane(jt),BorderLayout.SOUTH);

     JFrame cerceve=new JFrame(bb);

     cerceve.addWindowListener(new BasicWindowMonitor());

     cerceve.getContentPane().add(new JScrollPane(jpan));

     cerceve.pack();

     cerceve.setVisible(true);

             }

             

     public String atombalance()

     {String s=" |";

      for(int i=0;i<name.length;i++)

        {  if(name[i].length()==2) s+=name[i]+"   ";

                   else if(name[i].length()==2) s+=name[i]+"  ";

           else if(name[i].length()==3) s+=name[i]+" ";

           else if(name[i].length()>=4) s+=name[i];

        }

      s+="|b0  b1 |\n";

      for(int j=0;j<atomList.length;j++)

      {s+=atomsymbols[j]+"|";

       for(int i=0;i<name.length;i++)

       {s+=A[j][i]+" ";}

       s+=" |"+b0[j]+" "+b1[j]+"|\n";

      }

     return s;

     }

     public double Tadiabatic(double TR)

     {     double Taf=Taf(TR,298.0,2000.0);

     if(Taf>1999.0&&Taf<=2000.0 ) Taf=Taf(TR,298.0,3000.0);

     if(Taf>2999.9&&Taf<=3000.0) Taf=Taf(TR,298.0,4000.0);

     if(Taf>3999.9&&Taf<=4000.0) Taf=Taf(TR,298.0,5000.0);

     return Taf;

     }

     public double Taf(double TR,double xl,double xu)

     {

      double TR1,xl1,xu1;

      TR1=TR;xl1=xl;xu1=xu;

     // Adyabatic flame temperature using Bisection method

     // bisection method to find roots of zero energy change

     // Q=0

     // defination of variables :

     // xl : lower guess

     // xu : upper guess

     // xr : root estimate

     // es : stopping criterion

     // ea :approximate error

     // maxit : maximum iterations

     // iter  : number of iteration

     double test;

     double xr=0;

     double es,ea;

     double fxl=0,fxr=0;

     int maxit=500,iter=0;

     es=0.000001;

     ea=1.1*es;

     while((ea>es)&&(iter<maxit))

     {

     xr=(xl1+xu1)/2.0;

     iter++;

     if((xl1+xu1)!=0)

        { ea=Math.abs((xu1-xl1)/(xl1+xu1))*100;}

     fxl= H(TR,xl1);

     fxr= H(TR,xr);

     test= fxl*fxr;

     if(test==0.0)       ea=0;

     else if(test<0.0)  xu1=xr;

     else

       {

       xl1=xr;

       }

     } //end of while

        return xr;

     }

    

     double Vi(double TR,double TP,int Ni)

     {return -G(TR,TP)/(96487*Ni);}

             

             double Vi0(double TR,double TP,int Ni)

     {return -G0(TR,TP)/(96487*Ni);}

}

 

reactionTest7.java

import javax.swing.*;

import java.io.*;

 

public class reactiontest7

{

public static void main(String arg[]) throws IOException

{

String s[]={"co","o2","co2"};

double N[][]={{1.0,0.0},{0.5,0.0},{0.0,1.0}};

double Tproduct=3000.0;  // degree K

double Treactant=3000.0; // degree K

chemicalReaction cr=new chemicalReaction("CO equilibrium",s,N);

cr.equilibrium_print(Treactant,Tproduct);

}             

}

 

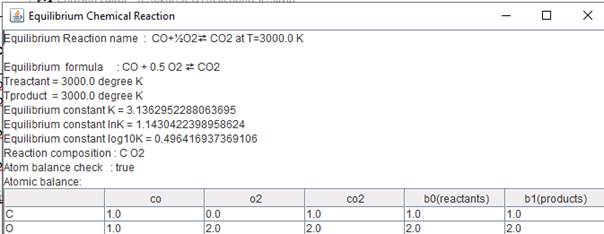
Now we can use this knowledge to calculate an equilibrium composition. For a better understanding of the process, we would like to solve an example problem by hand, before establishing a computer solution. One kmol of CO an done kmol of O2 established an equilibrium at 3000 K. The equilibrium reaction for this is as follows:

 

The reaction will be

CO+O2àn0CO+n1O2+n2CO2

Find the equilibrium composition. System pressure is P=1.01325 bar. (Pref=1.01325 bar)

The reaction will be

CO+O2àn0CO+n1O2+n2CO2

Find the equilibrium composition.

Atomic balance for C: 1=n0+n2

Atomic balance for O: 3=n0+2n1+2n2

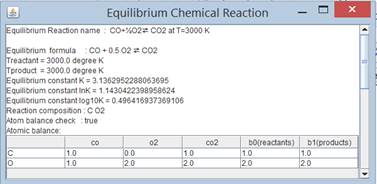
Equilibrium constant at T=3000 K :

K=3.1362952

   

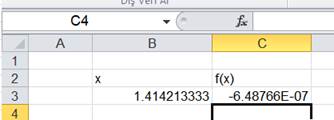
If this equation is solved by excel solver

n0=nCO

0.335081662

n1=nO2

0.667540831

n2=NCO

0.664918338

ntotal

1.667540831

lnK

1.143042231

 

-1.143042319

equation

-8.789E-08

 

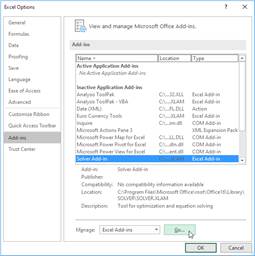
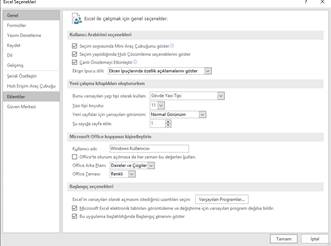
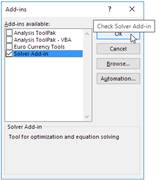
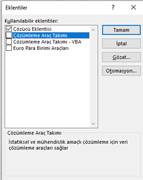
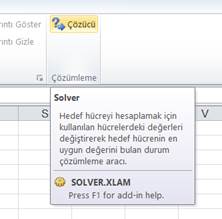
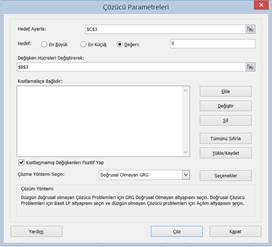
In excel, solver is existed to find real roots: We can use solver add in. In order to open solver:

On the File tab, click Options. (in turkish version dosya, seçenekler)

Under Add-ins(in turkish version eklentiler), select Solver Add-in (in turkish version Çözücü eklentisi),  and click on the Go(Git..) button.  You can find the Solver on the Data tab(Veri), in the Analyze group.

 

 

 

 

Now the same solution can be carried out by computer program. In order to solve the system a system of equation solver is used. For this purpose continuity method is used.

 

Below listed continuity method (it is also called homotophy method) to solve non-linear system of equation. This method is relatively less dependent to initial estimation of the system of equation solution, therefore a good selection for solving the system of non-linear equation. The method details is as follows:When a problem of system of nonlinear equations of the form F(x)=0 desired to be solved, assume that solution set to be found is x*. Consider a parametric function  G(l,x) in the form of

G(l,x) = lF(x) + (1-l)[ F(x) - F(x(0)) ]

Where l=0 coresponds to initial guess of the solution , x(0) ,and where l=1 value corresponds the actual solution set  x(1)= x*  

It is desired to be found  G(l,x) = 0 therefore for l=0 equation becomes

G(l,x) =G(0,x) =  F(x) - F(x(0))  and for l=1

0=G(1,x) =  F(x)

Therefore at x(1)=x* solution set will be obtained. If a function  G(l,x) satisfies the above equation can be found,  it will also find us the solution. Function G is called a homotopy between the function G(0,x) and G(1,x)=F(x). In order to find such a function, it is assumed to have a function

G(l,x)=0 is existed and partial derivative of this function with respect to l and x will also be zero

if x’(l) is isolated form this equation, it becomes:

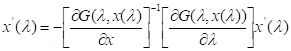
If G(l,x) = lF(x) + (1-l)[ F(x) - F(x(0)) ]  equation is substituted into the differential equation

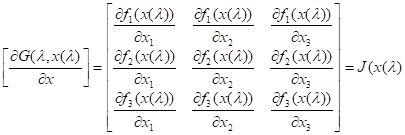
Forms a Jacobian matrix. and

Differential equation becomes

It is possible to solve such a differential equation by using initial value problem approaches, solution at x(1) will be given us the roots of the system of equation. Solutions of initial value problems will be given latter chapters in details, but A sixth order Runge-Kutta differential equation solution will be defined here to solve our homotopy problem. If equation

  is given the 6th order Runge-Kutta method to numerically solve this differential equation is defined as:

yi+1 = yi + (1/90)*( 7k1 + 32k3 +12k4+32k5+7k6)h

k1=f(xi,yi)

k2=f(xi+0.25h , yi+0.25k1h)

k3=f(xi+0.25h , yi+0.125k1h+0.125k2h)

k4=f(xi+0.5h , yi – 0.5k2h+k3h)

k5=f(xi+0.75h , yi + (3/16)k1h+(9/16)k4h)

k6=f(xi+h , yi - (3/7)k1h+(2/7)k2h+(12/7)k3h - (12/7)k4h+(8/7)k5h)

 

This equation can be given as Buthcher tableu as:

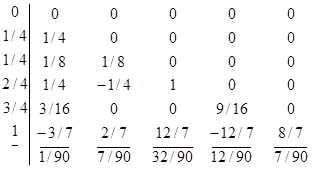
In these equations h is finite difference step size. Solution starts by using the initial value l=0 , x0(0) and adds h into l in each iteration step. The code given here uses 6th degree Runge-Kutta method to solve homotopy(Continuation problem).  It should be note that Homotophy method is less dependent to initial value compare to methods such as Newton-Raphson therefore one possibility is to approach solution with a relatively rough estimate with homotophy following with a Newton-Raphson type of method, which is quite efficient when the estimation approaches the correct roots.  In the following code methods of Homotophy with 6th order Runge-Kutta methods and combination of Homotophy with 4th order Runge-Kutta and Newton-Raphson method is given.

 

if_xj.java interface

@FunctionalInterface

interface  ifi_xj

{

  // multifunction multi independent variable

  // vector of dependent variables are returned

  // example f[0]=x[0]+sin(x[1])

  //         f[1]=x[0]*x[1]-x[1]

  // func(x) returns the value of f[0] and f[1]

  // as a two dimensional vector

  public double[] func(double x[]);

 

default  double[] xp(double x[],double j,double m,double h)

{

//h = dx

//j=-4..4 multiplication factor

//m derivative taken value

int k=x.length;

double xx[]=new double[k];

for(int i=0;i<k;i++)

{              if(i==m) xx[i]=x[i]+j*h;

    else     xx[i]=x[i];

}

return xx;

}

default double[][] dfunc(double x[])

{

double h=1.0e-12;

return dfunc(x,1,h);

}

default double[][] dfunc(double x[],int n)

{

double h=1.0e-12;

return dfunc(x,n,h);

}

 

default double[][] dfunc(double x[],int n,double h)

{

int k=x.length; //number of x values (dimension)

double df[][]=new double[k][k];

for(int i=0;i<k;i++)

{ for(int j=0;j<k;j++)

  {df[i][j]=dfunc(x,n,i,j,h);}

}

return df;

}

 

default double dfunc(double x[],int n,int j,int m)

{

double h=1.0e-12;

return dfunc(x,n,j,m,h);

}

 

default double dfunc(double x[],int n,int j,int m,double h)

{ // derivative of x[m]

  //m derivative taken value

  //jth equation

  //nth derivative of the equation (n=0) function value

  //n=1 first derivative n=2 second derivative..

int k=x.length; //number of x values (dimension)

double hh=1/h;

double ff[][]=new double[9][3];

double xp[][]=new double[9][3];

double df;

int j1;

double x1=0;

x1=x[m];

    for(int jj=-4;jj<=4;jj++)

    {  j1=jj+4;

                   xp[j1]=xp(x,jj,m,h);

       ff[j1]=func(xp[j1]);

    }

if(n==0)

{df=ff[4][j];}

else if(n==1)

{ df=(3.0*ff[0][j]-32.0*ff[1][j]+168.0*ff[2][j]-672.0*ff[3][j]+672.0*ff[5][j]-168.0*ff[6][j]+32.0*ff[7][j]-3.0*ff[8][j])/840.0*hh;}

else if(n==2)

{df=(-14350.0*ff[4][j]-9.0*ff[0][j]+128*ff[1][j]-1008*ff[2][j]+8064*ff[3][j]+8064.0*ff[5][j]-1008.0*ff[6][j]+128.0*ff[7][j]-9.0*ff[8][j])/5040.0*hh*hh;}

else if(n==3)

{df=(-7.0*ff[0][j]+72.0*ff[1][j]-338.0*ff[2][j]+488.0*ff[3][j]-488.0*ff[5][j]+338.0*ff[6][j]-72.0*ff[7][j]+7.0*ff[8][j])/240.0*hh*hh*hh;}

else if(n==4)

{df=(2730.0*ff[4][j]+7.0*ff[0][j]-96.0*ff[1][j]+676.0*ff[2][j]-1952.0*ff[3][j]-1952.0*ff[5][j]+676.0*ff[6][j]-96.0*ff[7][j]+7.0*ff[8][j])/240.0*hh*hh*hh*hh;}

else if(n==5)

{df=(ff[0][j]-9.0*ff[1][j]+26.0*ff[2][j]-29.0*ff[3][j]+29.0*ff[5][j]-26.0*ff[6][j]+9.0*ff[7][j]-ff[8][j])/6.0*hh*hh*hh*hh*hh;}

else if(n==6)

{df=(-150.0*ff[4][j]-ff[0][j]+12.0*ff[1][j]-52.0*ff[2][j]+116.0*ff[3][j]+116.0*ff[5][j]-52.0*ff[6][j]+12.0*ff[7][j]-ff[8][j])/4.0*hh*hh*hh*hh*hh*hh;}

else if(n==7)

{df=(-ff[0][j]+6.0*ff[1][j]-14.0*ff[2][j]+14.0*ff[3][j]-14.0*ff[5][j]+14.0*ff[6][j]-6.0*ff[7][j]+ff[8][j])/2.0*hh*hh*hh*hh*hh*hh*hh;}

else if(n==8)

{df=(70.0*ff[4][j]+ff[0][j]-8.0*ff[1][j]+28.0*ff[2][j]-56.0*ff[3][j]-56.0*ff[5][j]+28.0*ff[6][j]-8.0*ff[7][j]+ff[8][j])*hh*hh*hh*hh*hh*hh*hh*hh;}

else df=0;

return df;

}

 

}

 

Function f_equailibriumi.java

import java.io.*;

import java.util.*;

import javax.swing.*;

import java.awt.*;

import java.awt.event.*;

public class f_equilibriumi implements ifi_xj

{ public double n0[];

  public double n[];

  int nn,n1,n2;

  String name[];

  double TR,TP;

  public chemicalReaction cr;

  public double A[][];

  public double b[];

  public Gas g[];

  double Pref=1.01325;//bar

  double P;

  chemicalReaction chr[];

  public f_equilibriumi(double n0i[],String  namei[], chemicalReaction chri[],double T1i,double T2i,double Pi)

  { nn=n0i.length;

    int nn1=namei.length;

    if(nn!=nn1) System.out.println("array size error nn="+nn+"nn1="+nn1);

    P=Pi;

    n2=chri.length;

    n1=nn-n2;

   n0=new double[nn];

   n=new double[nn];

   g=new Gas[nn];

   name=new String[nn];

   TR=T1i;

   TP=T2i;

   chr=new chemicalReaction[n2];

   for(int i=0;i<n2;i++) {chr[i]=chri[i];}

   for(int i=0;i<nn;i++)

   {

                n0[i]=n0i[i];

    name[i]=namei[i];

    g[i]=new Gas(name[i]);

   }

   double N[][]=new double[nn][2];

   for(int i=0;i<nn;i++)

   {  N[i][0]=n0[i];

      N[i][1]=n[i];

   }

   cr=new chemicalReaction("base reaction",name,N);

   cr.conservation();

   A=cr.A;

   b=cr.b0;

  }

  public double[] func(double n[])

  { double b1[]=new double[nn];

    double nt=0;

    for(int i=0;i<nn;i++)

    {nt+=n[i];}

                for(int ii=0;ii<n1;ii++)

                { for(int ij=0;ij<nn;ij++)

      { double carpim=A[ii][ij]*n[ij];           

                               b1[ii]+=carpim;                       

      }

      b1[ii]=b1[ii]-b[ii];                                                                              

    }

    double lnK;

    double total;

    double mu[][]=new double[nn][2];

    double nx[];

    for(int ii=n1;ii<nn;ii++)

                {

                  int ij=ii-n1;

                  int nn2=chr[ij].ngas;

                  nx=new double[nn2];

                  for(int i=0;i<nn;i++)

         { 

                         for(int j=0;j<nn2;j++)

            {  if(name[i].equals(chr[ij].name[j]))

               {   mu[i][0]=chr[ij].N[j][0];mu[i][1]=chr[ij].N[j][1];

                   nx[j]=n[i];

                  

                               break;

                           }

           }

         }

                  total=0;

                  for(int i=0;i<chr[ij].ngas;i++)

      { if(nx[i]!=0)

        {total-=mu[i][0]*Math.log(nx[i]/nt*P/Pref);

         total+=mu[i][1]*Math.log(nx[i]/nt*P/Pref);

        }

                  }

      lnK=chr[ij].lnK(TR,TP);     

      b1[ii]=lnK-total;

                }             

   return b1;

  }

     public  void equilibrium_print(double ni[])

     {

                 double x[]=new double[nn];

                 double x0[]=new double[nn];

                 double nnt=0;

                 double nn0t=0;

                 for(int i=0;i<nn;i++){nnt+=ni[i];nn0t+=n0[i];}

                 for(int i=0;i<nn;i++){x[i]=ni[i]/nnt;x0[i]=n0[i]/nn0t;}

     JTextArea jta;

     JPanel jpan=new JPanel();

     jpan.setLayout(new BorderLayout());

     String s="";

     s+="Treactant = "+TR+" degree K\n";

     s+="Tproduct  = "+TP+ " degree K\n";

     s+="P         = "+P+" bar\n";

     s+="==========================================\n";

     for(int i=0;i<n2;i++)

     {

     s+="Equilibrium Reaction   : "+chr[i].toStringE()+"\n";

     s+="Equilibrium constant K = "+chr[i].K(TR,TP)+"\n";

     s+="Equilibrium constant lnK = "+chr[i].lnK(TR,TP)+"\n";

     s+="==========================================\n"; 

     }

    

     //for(int j=0;j<nn;j++)

     //{s+="n_"+name[j]+" = ["+n0[j]+" ,  "+ni[j]+" ]\n";}

     jta=new JTextArea(s);

    

     String heading[]={"name","n0 mole in","x0 mole ratio in","n mole out","x mole ratio out"};

     String s1[][]=new String[nn+1][5];    

     for(int i=0;i<nn;i++)

     {s1[i][0]=name[i];

      s1[i][1]=""+n0[i];

      s1[i][2]=""+x0[i];

      s1[i][3]=""+ni[i];

      s1[i][4]=""+x[i];

     }

     s1[nn][0]="total";

     s1[nn][1]=""+nn0t;

     s1[nn][2]=""+1;

     s1[nn][3]=""+nnt;

     s1[nn][4]=""+1;

                 JTable jt;

                 genelModel gm=new genelModel(s1,heading);

                 jt=new JTable(gm);

                  jpan.add(jta,BorderLayout.NORTH);

                  jpan.add(new JScrollPane(jt),BorderLayout.SOUTH);

                 String bb="Equilibrium Chemical Reaction";

                 JFrame cerceve=new JFrame(bb);

     cerceve.addWindowListener(new BasicWindowMonitor());

     cerceve.getContentPane().add(new JScrollPane(jpan));

     cerceve.pack();

     cerceve.setVisible(true);

                 }

 

Continuityi.java

import java.util.*;

import java.awt.*;

import java.applet.Applet;

import java.awt.event.*;

import javax.swing.*;

 

public class continuityi

{

// (Continuity-homotopy) method to solve a system of nonlinear equations

public static double[] multiply(double left,double[] right)

{

//multiplying a vector with a constant

int i;

int n=right.length;

double b[];

b=new double[n];

for(i=0;i<n;i++)

  {b[i]=left*right[i];}

return b;

}

public static double[] multiply(double[][] left,double[] right)

{

//multiplication of one matrix with one vector

int ii,jj,i,j,k;

int m1=left[0].length;

int n1=left.length;

int m2=right.length;

double[] b;

b=new double[m2];

 if(n1 != m2)

 {

 System.out.println("inner matrix dimensions must agree");

 for(ii=0;ii<n1;ii++)

   {

     b[ii]=0;

   }

   return b;

 }

 for(i=0;i<m1;i++)

   {

     b[i]=0;

     for(k=0;k<n1;k++)

                b[i]+=left[i][k]*right[k];

   }

return b;

//end of multiply of a matrix and a vector

}

public static double[] add(double[] left,double[] right)

{

//addition of two vectors

int n1=left.length;

int n2=right.length;

int nMax;

int i;

if(n1>=n2) nMax=n1;

else       nMax=n2;

double b[];

b=new double[nMax];

for(i=0;i<n1;i++)

  {

    b[i]=b[i]+left[i];

  }

for(i=0;i<n2;i++)

  {

    b[i]=b[i]+right[i];

  }

return b;

//end of vector addition method

}

public static double[][] inv(double[][] a)

{

// INVERSION OF A MATRIX

// inversion by using gaussian elimination

// with full pivoting

int n=a.length;

int m=a[0].length;

double b[][];

b=new double[n][n];

int indxc[];

int indxr[];

double ipiv[];

indxc=new int[n];

indxr=new int[n];

ipiv=new double[n];

int i,j,k,l,ll,ii,jj;

int icol=0;

int irow=0;

double big,dum,pivinv,temp;

if(n!=m)

{ System.out.println("Matrix must be square ");

                  for(ii=0;ii<n;ii++)

                    for(jj=0;jj<n;jj++)

                               b[ii][jj]=0.0;

                  return b;

}

for(i=0;i<n;i++)

   for(j=0;j<n;j++)

       b[i][j]=a[i][j];

for(i=0;i<n;i++)

{

  big=0.0;

  for(j=0;j<n;j++)

  {

    if(ipiv[j] != 1)

      for(k=0;k<n;k++)

      {

                if(ipiv[k] == 0)

                {

                  if(Math.abs(b[j][k]) >= big)

                  {

                    big=Math.abs(b[j][k]);

                    irow=j;

                    icol=k;

                  }

                }

                else if(ipiv[k] > 1 )

                  {

                  System.out.println("error : inverse of the matrix : singular matrix-1");

                  for(ii=0;ii<n;ii++)

                    for(jj=0;jj<n;jj++)

                               b[ii][jj]=0.0;

                  return b;

                  }

      }

  }

  ++ ipiv[icol];

  if(irow != icol)

    for(l=0;l<n;l++)

    {

    temp=b[irow][l];

    b[irow][l]=b[icol][l];

    b[icol][l]=temp;

    }

  indxr[i]=irow;

  indxc[i]=icol;

  if(b[icol][icol] == 0.0)

  {

    System.out.println("error : inverse of the matrix : singular matrix-2");

                  for(ii=0;ii<n;ii++)

                    for(jj=0;jj<n;jj++)

                               b[ii][jj]=0.0;

    return b;

  }

  pivinv=1.0/b[icol][icol];

  b[icol][icol]=1.0;

  for(l=0;l<n;l++) b[icol][l] *=pivinv;

  for(ll=0;ll<n;ll++)

  if(ll != icol)

  {

    dum=b[ll][icol];

    b[ll][icol]=0.0;

    for(l=0;l<n;l++) b[ll][l]-= b[icol][l]*dum;

  }

}

for(l=n-1;l>=0;l--)

{

  if(indxr[l] != indxc[l])

     for(k=0;k<n;k++)

     {

       temp=b[k][indxc[l]];

       b[k][indxc[l]]=b[k][indxr[l]];

       b[k][indxr[l]]=temp;

     }

}

return b;

}

public static double[] continuationRK6(ifi_xj f,double x[],int N)

{

//====================================================   

// Roots of nonlinear system of equations Homotophy RK6

// yi+1 = yi + (1/90)*( 7k1 + 32k3 +12k4+32k5+7k6)h

// k1=f(xi,yi)

// k2=f(xi+0.25h , yi+0.25k1h)

// k3=f(xi+0.25h , yi+0.125k1h+0.125k2h)

// k4=f(xi+0.5h , yi - 0.5k2h+k3h)

// k5=f(xi+0.75h , yi + (3/16)k1h+(9/16)k4h)

// k6=f(xi+h , yi - (3/7)k1h+(2/7)k2h+(12/7)k3h - (12/7)k4h+(8/7)k5h)

//===================================================

//x vector of independent variables

//y vector of dependent variables

//dy derivative vector of dependent variables

int i;

int nmax=1000;

double tolerance=1.0e-15;

int n=x.length;

double h=1.0/(double)N;

double b[]=new double[n];

double x1[]=new double[n];

double k[][]=new double[6][n];

double A[][]=new double[n][n];

b=multiply(-h,f.func(x));

for(i=0;i<N;i++)

{

A=f.dfunc(x);

// k1=f(xi,yi)

k[0]=multiply(inv(A),b);

x1=add(x,multiply(0.25,k[0]));

A=f.dfunc(x1);

// k2=f(xi+0.25h , yi+0.25k1h)

k[1]=multiply(inv(A),b);

x1=add(x,add(multiply(0.125,k[0]),multiply(0.125,k[1])));

A=f.dfunc(x1);

// k3=f(xi+0.25h , yi+0.125k1h+0.125k2h)

k[2]=multiply(inv(A),b);

x1=add(x,add(multiply(-0.5,k[1]),k[2]));

A=f.dfunc(x1);

// k4=f(xi+0.5h , yi - 0.5k2h+k3h)

k[3]=multiply(inv(A),b);

x1=add(x,add(multiply((3.0/16.0),k[0]),multiply((9.0/16.0),k[3])));

A=f.dfunc(x1);

// k5=f(xi+0.75h , yi + (3/16)k1h+(9/16)k4h)

k[4]=multiply(inv(A),b);

x1=add(x,

       add(multiply((-3.0/7.0),k[0]),add(multiply((2.0/7.0),k[1]),

       add(multiply((12.0/7.0),k[2]),

           add(multiply((-12.0/7.0),k[3]),multiply((8.0/7.0),k[4]))))));

A=f.dfunc(x1);

// k6=f(xi+h , yi - (3/7)k1h+(2/7)k2h+(12/7)k3h - (12/7)k4h+(8/7)k5h)

k[5]=multiply(inv(A),b);

// yi+1 = yi + (1/90)*( 7k1 + 32k3 +12k4+32k5+7k6)h

for(int j=0;j<n;j++) {x[j]=x[j]+1.0/90.0*(7.0*k[0][j]+32.0*k[2][j]+12.0*k[3][j]+32.0*k[4][j]+7.0*k[5][j]);}

}

return x;

}

public static double[] newton_continuationRK6(ifi_xj f,double x[])

{

// Roots of nonlinear system of equations Homotophy RK4 plus Newton-Raphson

//ti : weight function

//x vector of independent variables

//y vector of dependent variables

//dy derivative vector of dependent variables

x=continuationRK6(f,x,20);

double ti=1.0;

int i;

int nmax=1000;

double tolerance=1.0e-15;

int n=x.length;

double b[];

b=new double[n];

for(i=0;i<n;i++)

{

b[i]=1.0;

}

i=0;

while( i++ < nmax && Matrix.abs(b) > tolerance )

{ b=Matrix.multiply(Matrix.divide(f.func(x),f.dfunc(x)),-ti);

  x=Matrix.add(x,b);

}

if(i >= nmax) JOptionPane.showMessageDialog(null,"Warning : Maximum number of iterations are exceeded \n"+

              " Results may not be valid","MAXIMUM ITERATIONS WARNING",JOptionPane.WARNING_MESSAGE);

System.out.println();

return x;

}

public static double[] newton(ifi_xj f,double x[])

{

// Roots of nonlinear system of equations Homotophy RK4 plus Newton-Raphson

//ti : weight function

//x vector of independent variables

//y vector of dependent variables

//dy derivative vector of dependent variables

double ti=1.0;

int i;

int nmax=1000;

double tolerance=1.0e-15;

int n=x.length;

double b[];

b=new double[n];

for(i=0;i<n;i++)

{

b[i]=1.0;

}

i=0;

while( i++ < nmax && Matrix.abs(b) > tolerance )

{ b=Matrix.multiply(Matrix.divide(f.func(x),f.dfunc(x)),-ti);

  x=Matrix.add(x,b);

}

if(i >= nmax) JOptionPane.showMessageDialog(null,"Warning : Maximum number of iterations are exceeded \n"+

              " Results may not be valid","MAXIMUM ITERATIONS WARNING",JOptionPane.WARNING_MESSAGE);

System.out.println();

return x;

}

public static double[] enterdata()

{

    String s=JOptionPane.showInputDialog("enter initial root estimations with a space in between ");       

    StringTokenizer token=new StringTokenizer(s);

    int n=token.countTokens()-1;

    int m=n+1;

    double a[]=new double[m];

    int j=0;          

    while(token.hasMoreTokens())

    {

    Double ax=new Double(token.nextToken());

    a[j++]=ax.doubleValue();

    }

    return a;

}

  public static void main(String arg[])

  {   String s[]={"co","o2","co2"};

      double N[][]={{1.0,0.0},{0.5,0.0},{0.0,1.0}};

      chemicalReaction r[]=new chemicalReaction[1];

      r[0]=new chemicalReaction("r1",s,N);

      double Tproduct=3000.0;//degree K

      double Treactant=3000.0;//degree K

      double n0[]={1,1,0};

      double P=1.01325;//bar

                  f_equilibriumi fe=new f_equilibriumi(n0,s,r,Treactant,Tproduct,P); 

                  double n[]={0.3,0.3,0.3};

                  double [] r1= continuationRK6(fe,n,4);

                  String ss[]={"nCO","nH2O","nCO2","nH2","nO2"};

                  String ss1="Equilibrium reaction CO+"+'\u00BD'+"O2"+'\u21C4'+" CO2 \n";

                  double r2[]=fe.func(r1);

                  Text.print(r1,ss,ss1);

                  Text.print(r2,"function values");

  }

}

 

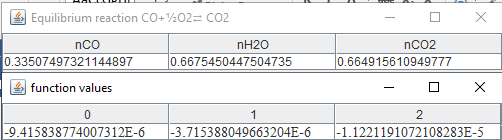
Of course other non-linear system solving methods are also available

1  NEWTON-RAPHSON METHOD

One dimensional Newton-Raphson Formula was:

                                         (4.1.1)

If the equation format changed a little, it can be written in the form of

                              (4.1.2)

                                     (4.1.3)

 

Now the same equation can be considered for a system of non-linear equation

  (4.1.4)             (4.1.5)

So multidimensional Newton-Raphson equation becomes

      (4.1.6)

The equation can be solved by using tecqniques such as gauss elimination. An initial estimate for all the x values are required to start iterative solution

 

 

// newtoni Newton Raphson method

// to solve non-lineer system of equation

 

import java.util.*;

import java.awt.*;

import java.applet.Applet;

import java.awt.event.*;

import javax.swing.*;

//============= Tanimi gereken fonksiyon ================

 

 

public class newtoni

{

// Roots of system of non-lineer equations

// By using Newton-Raphson Method

 

public static double[] newtond( ifi_xj f,double x[])

{

//x vector of independent variables

//y vector of dependent variable

//dy derivative of vector of dependent variable

// derivative vector calculated by numerical derivatives

double ti=1.0;

int i,ii,jj;

int nmax=500;

double tolerance=1.0e-15;

int n=x.length;

double b[];

b=new double[n];

double dy[][];

dy=new double[n][n];

i=0;

for(i=0;i<n;i++)

{

b[i]=1.0;

}

while( i++ < nmax && Matrix.abs(b) > tolerance )

{   b=Matrix.multiply(Matrix.divide(f.func(x),f.dfunc(x)),-ti);

    x=Matrix.add(x,b);

}

if(i >= nmax) JOptionPane.showMessageDialog(null,"Maximum number of iterations are exceeded \n"+

              " Results might not be valid","MAXIMUM NUMBER OF ITERATIONS ERROR",JOptionPane.WARNING_MESSAGE);

return x;

}

 

public static double[] verigir()

{

    String s=JOptionPane.showInputDialog("ENTER FIRST ROOT ESTIMATES WİTH ONE EMPTY SPPACE IN BETWEEN: ");       

    StringTokenizer token=new StringTokenizer(s);

    int n=token.countTokens()-1;

    int m=n+1;

    double a[]=new double[m];

    int j=0;          

    while(token.hasMoreTokens())

    {

    Double ax=new Double(token.nextToken());

    a[j++]=ax.doubleValue();

    }

    return a;

}

     public static void main (String args[]) 

     {String s[]={"co","o2","co2"};

      double N[][]={{1.0,0.0},{0.5,0.0},{0.0,1.0}};

      chemicalReaction r[]=new chemicalReaction[1];

      r[0]=new chemicalReaction("r1",s,N);

      double Tproduct=3000.0;//degree K

      double Treactant=3000.0;//degree K

      double n0[]={1,1,0};

      double P=1.01325;//bar

                  f_equilibriumi fe=new f_equilibriumi(n0,s,r,Treactant,Tproduct,P); 

                  double n[]={0.3,0.1,0.3};

     double [] r1= newtond(fe,n0);

     System.out.println(Matrix.toString(r1));

     /*

     String ss[]={"nCO","nH2O","nCO2","nH2","nO2"};

                  String ss1="Equilibrium reaction CO+"+'\u00BD'+"O2"+'\u21C4'+" CO2 \n";

                  double r2[]=fe.func(r1);

                  Text.print(r1,ss,ss1);

                  Text.print(r2,"function values");

                  */

     }

}

 

The same result is established in here as well. Now if conditions change, a new equilibrium condition will result. If the pressure applied in this problem becomes P=2 bar, the new equilibrium condition will be:

public class equilibriumi

{public static void main(String arg[])

  {   String s[]={"co","o2","co2"};

      double N[][]={{1.0,0.0},{0.5,0.0},{0.0,1.0}};

      chemicalReaction r[]=new chemicalReaction[1];

      r[0]=new chemicalReaction("r1",s,N);

      double Tproduct=3000.0;//degree K

      double Treactant=3000.0;//degree K

      double n0[]={1,1,0};

      double P=2.0;//bar

                  f_equilibriumi fe=new f_equilibriumi(n0,s,r,Treactant,Tproduct,P); 

                  double n[]={0.5,0.5,0.5};

                  double [] r1= continuityi.continuationRK6(fe,n,4);

                  String ss[]={"nCO","nH2O","nCO2","nH2","nO2"};

                  String ss1="Equilibrium reaction CO+"+'\u00BD'+"O2"+'\u21C4'+" CO2 \n";

                  double r2[]=fe.func(r1);

                  Text.print(r1,ss,ss1);

                  Text.print(r2,"function values");

  }

}

 

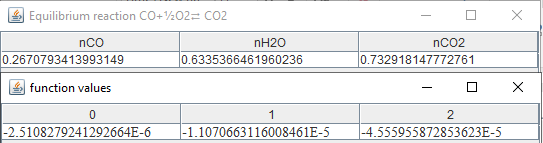
If the temperature drops to 2500 K for a pressure P=1.01325 bar:

public class equilibriumi

{public static void main(String arg[])

  {   String s[]={"co","o2","co2"};

      double N[][]={{1.0,0.0},{0.5,0.0},{0.0,1.0}};

      chemicalReaction r[]=new chemicalReaction[1];

      r[0]=new chemicalReaction("r1",s,N);

      double Tproduct=2500.0;//degree K

      double Treactant=2500.0;//degree K

      double n0[]={1,1,0};

      double P1.01325;//bar

                          f_equilibriumi fe=new f_equilibriumi(n0,s,r,Treactant,Tproduct,P); 

                          double n[]={0.5,0.5,0.5};

                          double [] r1= continuityi.continuationRK6(fe,n,4);

                          String ss[]={"nCO","nH2O","nCO2","nH2","nO2"};

                          String ss1="Equilibrium reaction CO+"+'\u00BD'+"O2"+'\u21C4'+" CO2 \n";

                          double r2[]=fe.func(r1);

                          Text.print(r1,ss,ss1);

                          Text.print(r2,"function values");

  }

}

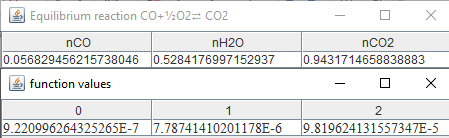
If the temperature drops to 2000 K for a pressure P=1.01325 bar:

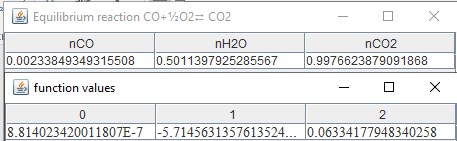
As you can  see from the results, CO vanishes when equilibrium temperature gets lower.

For T=3000 K and P=1.01325 bar, if N2 is added to the reaction. Equilibrium reaction is still the same:

 

The reaction will be

CO+O2+1.88N2àn0CO+n1O2+n2CO2+1.88N2

Find the equilibrium composition.

Atomic balance for C: 1=n0+n2

Atomic balance for O: 3=n0+2n1+2n2

Equilibrium constant at T=3000 K :

K=3.1362952

   

l

If this equation is solved by excel solver

n0=nCO

0.417734523

n1=nO2

0.708867261

n2=nCO

0.582265477

n3=nN2

1.88

ntotal

3.588867261

lnK

1.143042231

 

-1.143042181

equation

5.00389E-08

 

 

public class equilibriumi

{public static void main(String arg[])

  {   String s[]={"co","o2","co2","n2"};

      double N[][]={{1.0,0.0},{0.5,0.0},{0.0,1.0},{0,0}};

      chemicalReaction r[]=new chemicalReaction[1];

      r[0]=new chemicalReaction("r1",s,N);

      double Tproduct=3000.0;//degree K

      double Treactant=3000.0;//degree K

      double n0[]={1,1,0,1.88};

      double P=1.01325;//bar

                          f_equilibriumi fe=new f_equilibriumi(n0,s,r,Treactant,Tproduct,P); 

                          double n[]={0.5,0.5,0.5,1.88};

                          double [] r1= continuityi.continuationRK6(fe,n,4);

      fe.equilibrium_print(r1);

  }

}

 

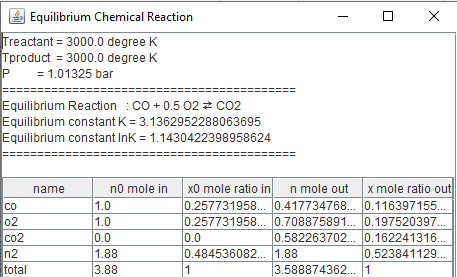
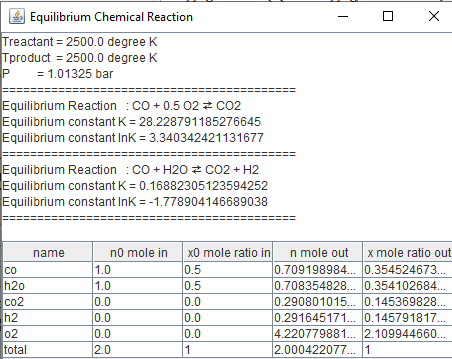
As it is seen from the example, inert gas that does not goes into the reaction, still changes the equilibrium composition.Now let us look at more than one simultaneous reactions going on together:One mole of CO and one mole of H2O are heated to 2500 K and 1.01325 bar. Determine the equilibrium composition if it is assumed that only CO, CO2, H2, H2O and O2 are presented.

public class equilibrium1i

{public static void main(String arg[])

  {   chemicalReaction r[]=new chemicalReaction[2];

      String s[]={"co","h2o","co2","h2","o2"};

      double N1[][]={{1.0,0.0},{0,0},{0,1},{0.0,0.0},{0.5,0.0}};

      r[0]=new chemicalReaction("r0",s,N1);

      double N2[][]={{1.0,0.0},{1.0,0.0},{0.0,1.0},{0.0,1.0},{0,0}};

      r[1]=new chemicalReaction("r1",s,N2);

      double Tproduct=2500.0;//degree K

      double Treactant=2500.0;//degree K

      double n0[]={1.0,1.0,0.0,0.0,0.0};

      double P=1.01325;//bar

              f_equilibriumi fe=new f_equilibriumi(n0,s,r,Treactant,Tproduct,P); 

              double n[]={0.5,0.5,0.5,0.5,0.5}; 

              double [] r1= continuityi.newton_continuationRK6(fe,n);

              String ss[]={"nCO","nH2O","nCO2","nH2","nO2"};

              String ss1="Equilibrium reaction CO+"+'\u00BD'+"O2"+'\u21C4'+" CO2 \n";

              ss1+="CO+"+"at T="+Tproduct+" K ";

              fe.equilibrium_print(r1);

 

  }

}

 

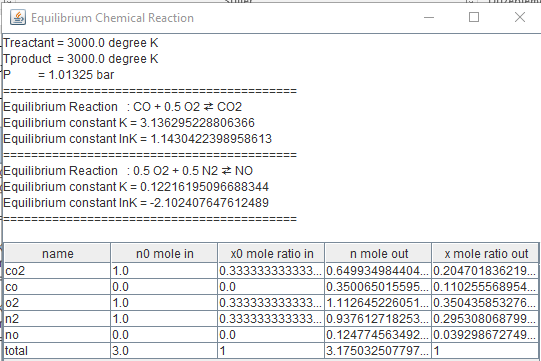
As a result of heating, a system consisting initially of 1 kmol of CO2, kmol of O2, and kmol of N2 forms an equilibrium mixture of CO2, CO, O2, N2, and NO at 3000 K, 1.01325 bar. Determine the composition of the equilibrium mixture.

 

public class equilibrium2i

{public static void main(String arg[])

  {   chemicalReaction r[]=new chemicalReaction[2];

      String s[]={"co2","co","o2","n2","no"};

      double N1[][]={{.0,1.0},{1,0},{0.5,0},{0.0,0.0},{0.0,0.0}};

      r[0]=new chemicalReaction("r0",s,N1);

      double N2[][]={{0.0,0.0},{0.0,0.0},{0.5,0.0},{0.5,0.0},{0,1}};

      r[1]=new chemicalReaction("r1",s,N2);

      double Tproduct=3000.0;//degree K

      double Treactant=3000.0;//degree K

      double n0[]={1.0,0.0,1.0,1.0,0.0};

      double P=1.01325;//bar

              f_equilibriumi fe=new f_equilibriumi(n0,s,r,Treactant,Tproduct,P); 

              double n[]={0.5,0.5,0.5,0.5,0.5}; 

              double [] r1= continuityi.newton_continuationRK6(fe,n);

              String ss[]={"nCO","nH2O","nCO2","nH2","nO2"};

              String ss1="Equilibrium reaction CO+"+'\u00BD'+"O2"+'\u21C4'+" CO2 \n";

              ss1+="CO+"+"at T="+Tproduct+" K ";

              fe.equilibrium_print(r1);

  }

}

 

 

ÖDEV PROBLEMLERİ

 

HW1: Water at 3000 K and P=1.01325 bar pressure dissociate to form some hydrogen and oxygen.

Calculate amount of O2 and H2 when systems came into equilibrium condition. Carry out this problem by hand and by using computer program

 

HW2: As a result of heating, a system consisting initially of 1 kmol of CO2, 1 kmol of O2, and 3.76 kmol of N2 forms an equilibrium mixture of CO2, CO, O2, N2, NO and NO2 at 3000 K, 1.01325 bar. Determine the composition of the equilibrium mixture. Carry out this problem by hand and by using computer program