6.1 Basics of combustion process
Most of the energy we
use today are based on a chemical reaction called combustion. Combustion
process requires a fuel, basically a hydrocarbon and oxidant (air or oxygen). Fuel and
oxidants together called reactants. When a chemical reaction occurs, the bonds
within molecules of the reactants are broken, and atoms and electrons
rearrange to form products.
In combustion reactions, rapid oxidation of combustible elements of the
fuel results in energy release as combustion products are formed. Fuel is
mostly made of Hydrogen and Carbon atoms, but some Sulfur and other trace
elements can also existed. In solid fuels also
non-combustible elements can exist. They can form solids after combustion which
is called ash. Combustion is complete when carbon atoms burned to
carbondioxide, hydrogen atoms burned to water and sulfur atoms burned to
sulfurdioxide, and all other combustible elements are fully oxidized. When this condition is not fulfilled
combustion is incomplete. Combustion reaction can be summarized as
Reactants à Products or fuel+oxidizeràProducts
As an oxidizer usuakky air is
used, except special cases like requirement of high temperatures. Air is a
complex mixture of several gases. Air composition is given in table 6.1.1
Table 6.1.1
Composition of atmospheric air
|
Name |
Formula |
Mol % |
|
Nitrogen |
N2 |
78.084 |
|
Oxygen |
O2 |
20.946 |
|
Argon |
Ar |
0.9340 |
|
Carbondioxide |
CO2 |
0.0397 |
|
Neon |
Ne |
0.001818 |
|
Helium |
He |
0.000524 |
|
Methane |
CH4 |
0.000179 |
|
Water vapor |
H2O |
0.00001-0.05 |
As it is seen from
the table major elements in composition is nitrogen, oxygen and argon. As
another simplification, we usually ignore argon as well and assume air
composition as 79 % N2 and 21% O2 or per kmole of O2
79/21=3.761905 kmol of N2 per kmole of oxygen. Nitrogen is
noncombustible in normal conditions, but it can be converted to nitrous oxides
in relatively small quantities. These are not significant in energy balance,
but has big enviromental effects.
It
is customary to write the reaction formula with one kmol of fuel input in reactions
such as: CH4 or (0.9CH4+0.2C2H6). When
combustion is complete and there are no excess oxygen
in products this type of reactions are called stoichiometric reactions. As an example
reaction, stoichiometric combustion reaction of methane(CH4) can
be given as follows:
CH4+2(O2+3.761905 N2)àCO2+2H2O+7.52381N2
As
it is seen from the equation, amount of nitrogen entered into reaction is
emerged exactly the same amount in products, oxygen is not existed in products
and carbon burned to carbondioxide and hydrogen burned to water. Amounts of
chemicals appeared in products are depends on the mass balances of the atoms.
Number of atomsa re conserved in reaction, so product mol numbers of molecules
are depends on the number of atoms in reactants. In above reaction one carbon atom went
into the reactions, therefore one carbondioxide appears in products, and 4
hydrogen atom went into reaction so two water molecules are emerged as a
result. From emerging CO2 and H2O, required O2
in the oxydant can be calculated to be 2 from O atomic balance
O balance ; 2x=2+2 x=2
Amount
of air going into the reaction is important concept in combustion. For the
above reaction
Amount
of air per kmol of fuel=2*(1+ 3.761905 )=9.52381 kmol air/kmol fuel. Enthalpy
definition for combustion process usually taken 298.16 degree K(25 degree C) as
reference point. Furthermore a state of enthalpy existed due to chemical potentials
of reactions. During a chemical reacton, some chemical bonds are broken, and a
new ones are formed. The chemical energy associated with these bonds are in
general is different. The energy level due to chemical reactions at the
reference temperature of 298.16 K is called enthalpy of formation. Since the
temperature in this defination is constatnt, it can be given as a single
reference value for each molecules in reaction. So enthalpy of a molecule going
into the reaction calculated as:
where 
is formation enthalpy and 
is the total enthalpy used in chemical reaction processes.
The first law of thermodynamic for a combustion states than
(6.1.1)
In this equation potential
and kinetic energy terms are ignored, equation simplified as:
(6.1.2)
The work term is only apply
to fuel cell type applications. If only a combustion chamber is considered,
work term can be considered zero and heat transfer of a combustion reaction
becomes:
(6.1.3)
when Ni is the mol
numbers of the molecules going into the reactions. Second hand side of the
equation is the enthalpy of the reaction
, (6.1.4)
similarly entropy of the
reaction can be written as
(6.1.5)
(6.1.6)
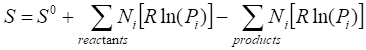(6.1.7)
Gibbs free energy of
reaction:
(6.1.8)
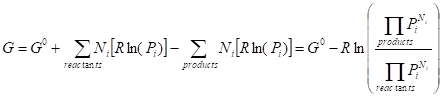(6.1.9)
As a first example heat
transfer for a reaction is calculated by using polynomial eqautions as a base
for Cp as:
Program 6.1.1 CH4 fuel combustion calculated in excel by using a 4th
degree polynomial functions
|
To
check the accuracy the same calculation can be repeated in java environment
Program 6.1.2 CH4 fuel combustion
calculated in java by using a 4th degree polynomial functions
|
public class reactiontest3 { static double ht(int i,double T) { double Tr=298.16; double R=8.3145; double C[][]= {{1.939869186926E+01,6.565333278907E-02,-1.466182490573E-05,-6.329616609155E-10,5.819409563279E-13,-5.116465644319E-17}, {2.675596850695E+01,1.150718911476E-02,-4.873333185805E-06,1.246226000157E-09,-1.649499826041E-13,8.822371434893E-18}, {2.794626725797E+01,3.608818970753E-03,2.154061888770E-06,-1.491279827848E-09,2.967027913986E-13,-1.949118588911E-17}, {2.385184692766E+01,5.407033093625E-02,-3.169416460166E-05,9.226660264546E-09,-1.296877816241E-12,7.020934713906E-17}, {3.174807138649E+01,4.957708828333E-03,7.949985639501E-06,-4.064180760029E-09,7.197141669681E-13,-4.404120668938E-17}}; double
hf[]={-74850.0,0.0,0.0,-393520.0,-241820.0}; double
hh=(C[i][0]*(T-Tr)+C[i][1]/2.0*(T*T-Tr*Tr)+C[i][2]/3.0*(T*T*T-Tr*Tr*Tr)+C[i][3]/4.0*(T*T*T*T-Tr*Tr*Tr*Tr)+C[i][4]/5.0*(T*T*T*T*T-Tr*Tr*Tr*Tr*Tr)+C[i][5]*(T*T*T*T*T*T-Tr*Tr*Tr*Tr*Tr*Tr))+hf[i]; return hh; } public static void main(String arg[]) { String
s[]={"ch4","o2","n2","co2","h2o"}; double N[][]={{1.0,0.0},{2.0,0.0},{7.523809524,7.523809524},{0.0,1.0},{0.0,2.0}}; double Tproduct=1000.0;//degree K double Treactant=298.16;//degree K int k=s.length; double Qproduct=0; double Qreactant=0; for(int i=0;i<k;i++) {
Qproduct+=N[i][1]*ht(i,Tproduct);} for(int i=0;i<k;i++) { Qreactant+=N[i][0]*ht(i,Treactant);} double Q=Qproduct-Qreactant; System.out.println("Q="+Q+" kW"); }} |
|
----------
Capture Output ---------- > "C:\java\bin\javaw.exe"
reactiontest3 Q=-553984.3967321854 kW > Terminated with exit code 0. |
Now we can calculate the same result with partially
continious curve fitting functions defined in Gas.java
class
Program 6.1.3 CH4 fuel combustion
calculated in java by using partial continous polynomial curve fitting with Gas
class
|
public
class reactiontest1 { public static void main(String arg[]) { String
s[]={"ch4","o2","n2","co2","h2o"}; double
N[][]={{1.0,0.0},{2.0,0.0},{7.523809524,7.523809524},{0.0,1.0},{0.0,2.0}}; double Tproduct=1000.0;//degree K double Treactant=298.16;//degree K int k=s.length; Gas g[]=new Gas[k]; for(int i=0;i<k;i++) {g[i]=new Gas(s[i]); } double Qproduct=0; double Qreactant=0; for(int i=0;i<k;i++) {Qproduct+=N[i][1]*g[i].ht(Tproduct);} for(int i=0;i<k;i++) {Qreactant+=N[i][0]*g[i].ht(Treactant);} double Q=Qproduct-Qreactant; System.out.println("Q="+Q); }} |
|
----------
Capture Output ---------- > "C:\java\bin\javaw.exe"
reactiontest1 Q=-555419.69706795 > Terminated with exit code 0. |
As it is seen from the results there are the
difference in results. To check accuracy the same program can also be run by
using cubic spline curve fitting version of the ideal gas equation of state.
Program 6.1.4 CH4 fuel combustion
calculated in java by using cubic spline curve fitting with GasCS class
|
public
class reactiontest1CS { public static void main(String arg[]) { String
s[]={"ch4","o2","n2","co2","h2o"}; double
N[][]={{1.0,0.0},{2.0,0.0},{7.523809524,7.523809524},{0.0,1.0},{0.0,2.0}}; double Tproduct=1000.0;//degree K double Treactant=298.16;//degree K int k=s.length; GasCS g[]=new GasCS[k]; for(int i=0;i<k;i++) {g[i]=new GasCS(s[i]); } double Qproduct=0; double Qreactant=0; for(int i=0;i<k;i++) {Qproduct+=N[i][1]*g[i].ht(Tproduct);} for(int i=0;i<k;i++) {Qreactant+=N[i][0]*g[i].ht(Treactant);} double Q=Qproduct-Qreactant; System.out.println("Q="+Q); } } |
|
----------
Capture Output ---------- > "C:\java\bin\javaw.exe"
reactiontest1CS Q=-555425.1381705669 > Terminated with exit code 0. |
The results indicated that partially continious
curve fitting and cubic spline curve fitting function results are close enough
so both can be utilized for practical purposes, but single polynomial curve
fitting error levels indicates to be bigger.
What would happened if combustion product teperature
is 298.16 K as well? The value obtained for this case is called heating
value of the fuel. Result by using program 6.1.4 will be
|
----------
Capture Output ---------- > "C:\java\bin\javaw.exe"
reactiontest1CS Q=-802300.9008195192 > Terminated with exit code 0. |
There is only one problem here, at 298.16 K the
water in product will condense to liquid form, therefore the enthalpy of
evaporation should also be considered (of course at 298.16 K value) in the
equation
Program 6.1.5 CH4 fuel heating value
calculated in java by using cubic spline curve fitting with GasCS class with
liquid water exit
|
public
class reactiontest2CS { public static void main(String arg[]) { String
s[]={"ch4","o2","n2","co2","h2ol"}; double
N[][]={{1.0,0.0},{2.0,0.0},{7.523809524,7.523809524},{0.0,1.0},{0.0,2.0}}; double Tproduct=298.16;//degree K double Treactant=298.16;//degree K int k=s.length; GasCS g[]=new GasCS[k]; for(int i=0;i<k;i++) {g[i]=new GasCS(s[i]); } double Qproduct=0; double Qreactant=0; for(int i=0;i<k;i++) {Qproduct+=N[i][1]*g[i].ht(Tproduct);} for(int i=0;i<k;i++) {Qreactant+=N[i][0]*g[i].ht(Treactant);} double Q=Qproduct-Qreactant; System.out.println("Q="+Q); } } |
|
----------
Capture Output ---------- > "C:\java\bin\javaw.exe"
reactiontest2CS Q=-890308.9008195192 > Terminated with exit code 0. |
As it is seen from the result the value is higher
now. Logically at this temperature range water should condense in the product,
therefore the second result is the actual value of maximum possible heat
transfer from a combustion reaction. It is called higher heating value. For
commercial purposes, people also use the first assumption (vapor phase of the
water output at 298.16 K) and it is called lower heating value. By taking
referance point of lower heating value and condensing type boilers some
manufacturers claims that their boiler efficiency is more than 100%., which is of course a false claim.
Another limit in combustion is adiabatic flame
temperature. If combustion gases is
heated by the reaction and no heat is ejected from the reaction, products will
reach to a maximum temperature with zero heat transfer .
This limit is called adiabatic flame temperature. Curve fitting should applied to find this
limit value.
Program 6.1.6 CH4 adiabatic flame
temperature calculated in java by using bisection curve fitting with Gas class
|
import javax.swing.*; public class reactiontest4 { public static double Q(String s[],double
N[][],double Treactant,double Tproduct) {int k=s.length; Gas g[]=new Gas[k]; for(int i=0;i<k;i++) {g[i]=new Gas(s[i]); } double Qproduct=0; double Qreactant=0; for(int i=0;i<k;i++) {Qproduct+=N[i][1]*g[i].ht(Tproduct);} for(int i=0;i<k;i++) {Qreactant+=N[i][0]*g[i].ht(Treactant);} double Q=Qproduct-Qreactant; return Q; } public static double Tadiabatic(String s[],double
N[][],double Treactant,double Tproduct_low,double
Tproduct_high) { //bisection root finding method double xl=Tproduct_low; double xu=Tproduct_high; double test; double xr=0; double es,ea; double fxl,fxr; int maxit=100,iter=0; es=0.0000001; ea=1.1*es; while((ea>es)&&(iter<maxit)) {
xr=(xl+xu)/2.0; iter++;
if((xl+xu)!=0) {
ea=Math.abs((xu-xl)/(xu+xl))*100;} fxl=
Q(s,N,Treactant,xl); fxr=
Q(s,N,Treactant,xr); test= fxl*fxr;
if(test==0.0) ea=0; else if(test<0.0)
xu=xr; else
{xl=xr;} } if(iter>=maxit) JOptionPane.showMessageDialog(null,"Maximum
number of iteration is exceeded \n"+ "
result might not be valid","MAKSİMUM NUMBER OF ITERATION
WARNING",JOptionPane.WARNING_MESSAGE); return xr; } public static void main(String arg[]) { String
s[]={"ch4","o2","n2","co2","h2o"}; double
N[][]={{1.0,0.0},{2.0,0.0},{7.523809524,7.523809524},{0.0,1.0},{0.0,2.0}}; double Tproduct=1000.0;//degree K double Treactant=298.16;//degree K double
Tadiabatic=Tadiabatic(s,N,Treactant,298.16,3000.0); double Q=Q(s,N,Treactant,Tadiabatic); System.out.println("Tadiabatic="+Tadiabatic); System.out.println("Q="+Q); } } |
|
----------
Capture Output ---------- > "C:\java\bin\javaw.exe"
reactiontest4 Tadiabatic=2326.6911578521513 Q=-2.3041048552840948E-4 > Terminated with exit code 0. |
In order to make this calculations more formal, a
chemical reaction class is created and listed in appendix 8.1 By using this
class we can give the gas composition directly or it can be read from a file
called Reaction.txt through
a given reaction name.
Program 6.1.7 CH4 combustion calculated in
java by using class chemicalReaction in A8.1
|
import javax.swing.*; import java.io.*; public class reactiontest6 { public static void main(String arg[]) throws
IOException { String
s[]={"ch4","o2","co2","h2o","n2"}; double N[][]={{1.0,0.0},{2.0,0.0},{0.0,1.0},{0.0,2.0},{2.0*79/21,2.0*79/21}}; double Tproduct=1000.0;//degree K double Treactant=298.15;//degree K chemicalReaction cr=new chemicalReaction("CH4
combustion",s,N); cr.print(Treactant,Tproduct); } } |
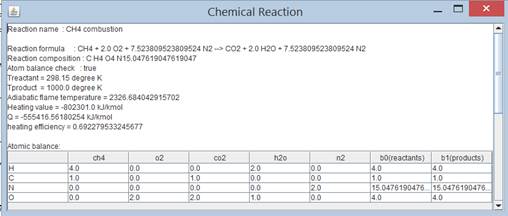
A common thing we have done
so far, is used the general reaction concepts. In doing so we have to give all
coefficients of the reaction. Combustion is a special chemical raction and it
happens between a fuel and oxydant(normally air), therefore, instead of giving
all constants, fuel combination and amount of air can be given to maket he
basic calculations. A class called combustion is developed for this purpose and
program list is given in appendix 8.2. Let us try program in the same example
program.
Program 6.1.8 CH4 adiabatic flame
temperature and reaction calculated in java by using class combustion in A8.2
|
import javax.swing.*; import java.io.*; public class combustiontest { public static void main(String arg[]) { String s[]={"ch4"}; double N[]={1.0}; double a_f=1.0; double Tproduct=1000.0;//degree K double Tfuel=298.16;//degree K double Tair=298.16;//degree K combustion cc=new combustion("CH4
combustion",s,N,a_f); System.out.println(cc.toString()); double Tadiabatic=cc.Taf(Tfuel,Tair,298.16,3000.0); double Q=cc.H(Tfuel,Tair,Tproduct); System.out.println("Tadiabatic="+Tadiabatic); System.out.println("Q="+Q); }} |
|
----------
Capture Output ---------- > "C:\java\bin\javaw.exe"
combustiontest [CH4] + 2.0000*[ O2 + (79/21) *N2] --> CO2 +
2.0000 H2O + 7.5238 N2 Tadiabatic=2326.691141496301 Q=-555419.6970720381 > Terminated with exit code 0. |
More complex reactions can also be given. For
example 10% excess air for 90% ch4 and 10% c2h6 fuel will give:
|
----------
Capture Output ---------- > "C:\java\bin\javaw.exe"
combustiontest [0.9000 CH4 + 0.1000 C2H6] + 2.3650*[ O2 + (79/21)
*N2] --> 1.1000 CO2 + 2.1000 H2O + 8.8969 N2 + 0.2150 O2 Tadiabatic=2196.5441922754053 Q=-577682.314331347 > Terminated with exit code 0. |
10% depleted air for 90% ch4 and 10% c2h6 fuel will
give:
|
----------
Capture Output ---------- > "C:\java\bin\javaw.exe"
combustiontest [0.9000 CH4 + 0.1000 C2H6] + 1.9350*[ O2 + (79/21)
*N2] --> 0.6700 CO2 + 2.1000 H2O + 7.2793 N2 + 0.4300 CO Tadiabatic=2224.182699812055 Q=-500631.88144321425 > Terminated with exit code 0. |
CO apeared in the last reaction, because there are
not enough oxygen existed for completed reaction.
FUELS AND COMBUSTION HOMEWORK #1
HOMEWORK 1
Fuel %80 CH4+%20CO is given. Reactants temperature is 298 K, and product temperature is 1000 K. Find
a) Assuming stoichiametric reaction calculate total heat transfer
b)
Assuming %30 excess air calculate total heat
transfer
c)
Assuming -%10 excess air (%10 less
than stoichiometric air) calculate total heat transfer
d)
Calculate lower and upper heating
values
e) Calculate adiabatic flame temperature
HOMEWORK 2
Fuel %20 C02+%80CO is given. Reactants
temperature is 298 K, and product temperature is 1000 K. Find
a)
Assuming stoichiametric reaction
calculate total heat transfer
b)
Assuming %30 excess air calculate total heat
transfer
c)
Assuming -%10 excess air (%10 less
than stoichiometric air) calculate total heat transfer
d)
Calculate lower and upper heating
values
e) Calculate adiabatic flame temperature
|
import javax.swing.*; public class reactiontest4 { public static double Q(String s[],double
N[][],double Treactant,double Tproduct) {int k=s.length; Gas g[]=new Gas[k]; for(int i=0;i<k;i++) {g[i]=new Gas(s[i]); } double Qproduct=0; double Qreactant=0; for(int i=0;i<k;i++) {Qproduct+=N[i][1]*g[i].ht(Tproduct);} for(int i=0;i<k;i++) {Qreactant+=N[i][0]*g[i].ht(Treactant);} double Q=Qproduct-Qreactant; return Q; } public static double Tadiabatic(String s[],double
N[][],double Treactant,double Tproduct_low,double
Tproduct_high) { //bisection root finding method double xl=Tproduct_low; double xu=Tproduct_high; double test; double xr=0; double es,ea; double fxl,fxr; int maxit=100,iter=0; es=0.0000001; ea=1.1*es; while((ea>es)&&(iter<maxit)) {
xr=(xl+xu)/2.0; iter++;
if((xl+xu)!=0) {
ea=Math.abs((xu-xl)/(xu+xl))*100;} fxl=
Q(s,N,Treactant,xl); fxr=
Q(s,N,Treactant,xr); test= fxl*fxr;
if(test==0.0) ea=0; else if(test<0.0)
xu=xr; else
{xl=xr;} } if(iter>=maxit) JOptionPane.showMessageDialog(null,"Maximum
number of iteration is exceeded \n"+ "
result might not be valid","MAKSİMUM NUMBER OF ITERATION
WARNING",JOptionPane.WARNING_MESSAGE); return xr; } public static void main(String arg[]) { String
s[]={"ch4","o2","n2","co2","h2o"}; double
N[][]={{1.0,0.0},{2.0,0.0},{7.523809524,7.523809524},{0.0,1.0},{0.0,2.0}}; double Tproduct=1000.0;//degree K double Treactant=298.16;//degree K double
Tadiabatic=Tadiabatic(s,N,Treactant,298.16,3000.0); double Q=Q(s,N,Treactant,Tadiabatic); System.out.println("Tadiabatic="+Tadiabatic); System.out.println("Q="+Q); } } |