6.3 Chemical equilibrium with Gibbs free energy minimisation

Defining equilibrium equations each time is a time consuming process. Instead, gibss free energy for the full reaction can be minimised to obtain an equilibrium state. Total Gibbs free energy of the reaction can be defined as:

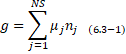
In this equation g is gibbs free energy and NS is the number of species in the reaction, m is chemical potential, and n_j is mole number for jth species. Chemical potential per kilomol j is defined to be

The condition for chemical equilibrium is the minimization of free energy. The minimisation is usually subject to certain constraints, such as the following mass-balance constraints:

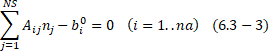
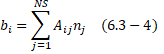
where na is the number of chemical elements. A_ij is number of kilogram atoms per kmole of species j. And is the assigned number of kilogram atoms element i per kmol of total reactants.

In order to explain this equation let us look at an example. If chemicals in the reaction and input moles re given as:

CH4	1 kmol
H2O	10 kmol
H2	0 kmol
CO2	0 kmol
CO	0 kmol
O2	0 kmol

A_ij matrix will be

atom	CH4	H2O	H2	CO2	CO	O2
H	4	2	2	0	0	0
C	1	0	0	1	1	0
O	0	1	0	2	1	2

vector is the multiplication of number of atoms with inlet mole numbers of the molecule

=1*4+10*2+0*2+0*0+0*0+0*0=24

=1*1+10*0+0*0+0*1+0*1+0*0=1

=0*1+10*1+0*0+0*2+0*1+0*2=10

In this case initial matrix will be in the form of:

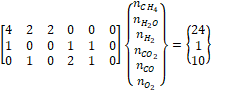
Assuming ideal gas:

So gibbs free energy equation that we will minimise will be:

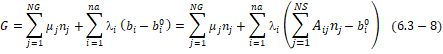
Where are lagrangian multipliers. The minimum value of the equation will give solution, but this equation is quite non-linear and relatively difficult to solve. We would like to introduce NASA method to solve the equation in here. The condition for equilibrium becomes:

Treating the variations dn_j and dl_i as independent variables gives

and

By opening these equations to Taylor series and simplification the following set of equations are obtained:

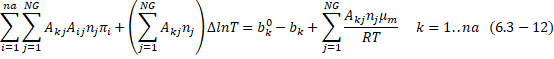
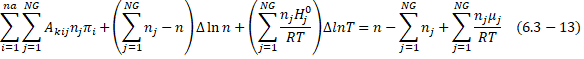
Where , (6.3.12) is the standart molar enthalpy for species j at temperature T. A program called gibbs.java is developed to solve this set of equations.

Program 6.3.1 gibbs.java

import java.io.*;

import java.util.*;

import javax.swing.*;

import java.awt.*;

import java.awt.event.*;

public class gibbs {

double[][] A;

gibbsSpecies[] gs;

double[][] n0;

double[][] n00;

double[][] n;

double[][] del_lnnm;

double[][] del_nm;

double[][] lnnm;

double nt;

double lnnt;

double del_lnnt;

int NG;//Gas species number

int l;//element number

double[][] d_coeff;

double[][] d_const;

double[][] b0;

double[][] b;

double[][] mu;

double[] mutemp;

double P;

double T;

double T0;

double[] Te;

double lambda;

double lambda1;

double lambda2;

double etemp=0;

double Tref=298.15;

double G=0;

double Gnew=0;

double diff=0;

double SIZE=25.328436;//18.420681;

double ntahminilk;

int it_max=100;

int it_max0=100;

int o2=-1;

int n2=-1;

//double[] error=new double[];

public gibbs(gibbsSpecies[] igs,double[][] in0,double iT,double iP){

int nn=igs.length;

int nat=110;

double B[][]=new double[nat][nn];

int nk=0;

for(int i=0;i<nn;i++)

{ for(nk=0;nk<igs[i].atomList.length;nk++){B[igs[i].atomList[nk].number-1][i]=igs[i].atomList[nk].N;}}

int natcount=0;

boolean zeroflag[]=new boolean[110];

for(int j=0;j<nat;j++)

{zeroflag[j]=false;for(int i=0;i<nn;i++){if(B[j][i]!=0){zeroflag[j]=true;}};if(zeroflag[j]) natcount++;}

A=new double[natcount][nn];

int k=0;

for(int j=0;j<nat;j++)

{if(zeroflag[j]){A[k]=B[j];k++;}}

n0=in0;

n00=new double[n0.length][1];

for(int i=0;i<n0.length;i++) n00[i][0]=in0[i][0];

gs=igs;

P=iP;

T=iT;

for(int i=0;i<in0.length;i++) Te[i]=iT;

mu=new double[gs.length][1];

mutemp=new double[gs.length];

l=A.length;

NG=A[0].length;

//n=n0;

//n=in;

lambda=1;

del_lnnm=new double[NG][1];

del_nm=new double[NG][1];

lnnm=new double[NG][1];

d_coeff=new double[l+1][l+1];

d_const=new double[l+1][1];

b=new double[l][1];

nt=getnt(n0);

ntahminilk=nt/n0.length;

n=new double[n0.length][1];

for(int i=0;i<n0.length;i++)

{n[i][0]=ntahminilk;}

nt=getnt(n);

b0=new double[l][1];

for(int ii=0;ii<b0.length;ii++){

for(int ij=0;ij<NG;ij++){

b0[ii][0]+=A[ii][ij]*n0[ij][0];

}

}

calMu(n0);

}

public gibbs(String igs[],double[][] in0,double iT,double iP,int iit_max)

{

it_max=iit_max;

it_max0=it_max;

Te=new double[in0.length];

for(int i=0;i<in0.length;i++) Te[i]=iT;

setgibbs(igs,in0,iT,iP);

}

public gibbs(String igs[],double[][] in0,double iT,double iP,int iit_max,double[][] in)

{

P=iP;

it_max=iit_max;

it_max0=it_max;

n=in;

Te=new double[in0.length];

for(int i=0;i<in0.length;i++) Te[i]=iT;

setgibbs(igs,in0,iP);

}

public gibbs(String igs[],double[][] in0,double iTe[],double iT,double iP)

{

it_max=500;

it_max0=it_max;

Te=new double[iTe.length];

for(int i=0;i<iTe.length;i++)

Te[i]=iTe[i];

setgibbs(igs,in0,iT,iP);

}

public gibbs(String igs[],double[][] in0,double iTe[],double iT,double iP,int iit_max){

it_max=iit_max;

it_max0=it_max;

Te=new double[iTe.length];

for(int i=0;i<iTe.length;i++)

Te[i]=iTe[i];

setgibbs(igs,in0,iT,iP);

}

public gibbs(String igs[],double[] inx0,double iTe[],double iT,double iP,int iit_max){

setgibbs(igs,inx0,iTe,iT,iP,iit_max);}

public gibbs(String igs[],double[] inx0,double iTe[],double iT,double iP){

setgibbs(igs,inx0,iTe,iT,iP,100);}

public void setgibbs(String igs[],double[] inx0,double iTe[],double iT,double iP,int iit_max){

it_max=iit_max;

it_max0=it_max;

Te=new double[iTe.length];

for(int i=0;i<iTe.length;i++)

Te[i]=iTe[i];

double[][] in0=new double[inx0.length][1];

for(int i=0;i<inx0.length;i++)

{in0[i][0]=inx0[i];}

setgibbs(igs,in0,iT,iP);

}

public double set_Q(String igs[],double[] inx0,double iTe[],double Q,double iP,int iit_max)

{

setgibbs(igs,inx0,iTe,1000.0,iP,iit_max);

double T1=Tad(Q);

setgibbs(igs,inx0,iTe,T1,iP,iit_max);

return T1;

}

public double set_Q(String igs[],double[] inx0,double iTe[],double Q,double iP)

{return set_Q(igs,inx0,iTe,Q,iP,500);}

public void setgibbs(String igs[],double[] inx0,double iTe[],double iT,double iP)

{ setgibbs(igs,inx0,iTe,iT,iP,500);}

public void setgibbs(String igs[],double[][] in0,double iT,double iP){

gs=new gibbsSpecies[igs.length];

for(int i=0;i<igs.length;i++){

gs[i]=new gibbsSpecies(igs[i],"gas");

}

int nn=igs.length;

int nat=110;

double B[][]=new double[nat][nn];

int nk=0;

for(int i=0;i<nn;i++){

for(nk=0;nk<gs[i].atomList.length;nk++){

B[gs[i].atomList[nk].number-1][i]=gs[i].atomList[nk].N;

}

}

int natcount=0;

boolean zeroflag[]=new boolean[110];

for(int j=0;j<nat;j++)

{zeroflag[j]=false;for(int i=0;i<nn;i++){if(B[j][i]!=0){zeroflag[j]=true;}};if(zeroflag[j]) natcount++;}

A=new double[natcount][nn];

int k=0;

for(int j=0;j<nat;j++)

{if(zeroflag[j]){A[k]=B[j];k++;}}

n0=in0;

n00=new double[n0.length][1];

for(int i=0;i<n0.length;i++) n00[i][0]=in0[i][0];

P=iP;

T=iT;

T0=iT;

mu=new double[gs.length][1];

mutemp=new double[gs.length];

l=A.length;

NG=A[0].length;

lambda=1;

del_lnnm=new double[NG][1];

del_nm=new double[NG][1];

lnnm=new double[NG][1];

d_coeff=new double[l+1][l+1];

d_const=new double[l+1][1];

b=new double[l][1];

nt=getnt(n0);

ntahminilk=nt/n0.length;

n=new double[n0.length][1];

for(int i=0;i<n0.length;i++){

n[i][0]=ntahminilk;

}

nt=getnt(n);

b0=new double[l][1];

for(int ii=0;ii<b0.length;ii++){

for(int ij=0;ij<NG;ij++){

double carpim=A[ii][ij]*n0[ij][0];

b0[ii][0]+=carpim;

}

}

calMu(n0);

}

public void setgibbs(String igs[],double[][] in0,double iP){

gs=new gibbsSpecies[igs.length];

for(int i=0;i<igs.length;i++){

gs[i]=new gibbsSpecies(igs[i],"gas");

}

int nn=igs.length;

int nat=110;

double B[][]=new double[nat][nn];

int nk=0;

for(int i=0;i<nn;i++){

for(nk=0;nk<gs[i].atomList.length;nk++){

B[gs[i].atomList[nk].number-1][i]=gs[i].atomList[nk].N;

}

}

int natcount=0;

boolean zeroflag[]=new boolean[110];

for(int j=0;j<nat;j++)

{zeroflag[j]=false;for(int i=0;i<nn;i++){if(B[j][i]!=0){zeroflag[j]=true;}};if(zeroflag[j]) natcount++;}

A=new double[natcount][nn];

int k=0;

for(int j=0;j<nat;j++)

{if(zeroflag[j]){A[k]=B[j];k++;}}

n0=in0;

n00=new double[n0.length][1];

for(int i=0;i<n0.length;i++) n00[i][0]=in0[i][0];

P=iP;

mu=new double[gs.length][1];

mutemp=new double[gs.length];

l=A.length;

NG=A[0].length;

lambda=1;

del_lnnm=new double[NG][1];

del_nm=new double[NG][1];

lnnm=new double[NG][1];

d_coeff=new double[l+1][l+1];

d_const=new double[l+1][1];

b=new double[l][1];

nt=getnt(n0);

ntahminilk=nt/n0.length;

n=new double[n0.length][1];

for(int i=0;i<n0.length;i++){

n[i][0]=ntahminilk;

}

nt=getnt(n);

b0=new double[l][1];

for(int ii=0;ii<b0.length;ii++){

for(int ij=0;ij<NG;ij++){

b0[ii][0]+=A[ii][ij]*n0[ij][0];

System.out.println(b0[ii][0]);

}

}

//calMu(n0);

}

public void setN0(double[][] in0)

{

//n00=new double[n0.length][1];

for(int i=0;i<n0.length;i++) n0[i][0]=in0[i][0];

}

public void setN0Default()

{

//n00=new double[n0.length][1];

for(int i=0;i<n0.length;i++) n0[i][0]=n00[i][0];

b0=getb(n00);

}

public void setT(double iTeq)

{

T=iTeq;

calMu(n0);

}

public void setTDefault()

{

T=T0;

}

public void setNmax(int iit_max){ it_max=iit_max;}

public void setNmaxDefault(){

it_max=it_max0;

}

public void getEq(){

//System.out.println(l+" "+NG);

nt=getnt(n0);

ntahminilk=nt/n0.length;

for(int i=0;i<n0.length;i++){

n[i][0]=ntahminilk;

}

nt=getnt(n);

b0=getb(n0);

double emax=1e-13;

double etest=1;

int it_counter=0;

double temp1=0;

double temp2=0;

lnnt=0;

for(int i=0;i<gs.length;i++) gs[i].getmu0(T,P);

while(it_counter<it_max && etest>emax){

temp1=0;

for(int k=0;k<l;k++){

for(int i=0;i<l;i++){

for(int j=0;j<NG;j++){

temp1+=A[k][j]*A[i][j]*n[j][0];

}

d_coeff[k][i]=temp1;

temp1=0;

}

}

for(int k=0;k<l;k++){

for(int j=0;j<NG;j++){

temp2+=A[k][j]*n[j][0];

}

d_coeff[k][l]=temp2;

temp2=0;

}

temp1=0;

temp2=0;

for(int i=0;i<l;i++){

for(int j=0;j<NG;j++){

temp1+=A[i][j]*n[j][0];

}

d_coeff[l][i]=temp1;

temp1=0;

}

d_coeff[l][l]=getnt(n)-nt;

b=getb(n);

calMu(n);

for(int k=0;k<l;k++) {

for(int j=0;j<NG;j++){

temp1+=A[k][j]*n[j][0]*mu[j][0]/(8.3145*T);

}

d_const[k][0]=b0[k][0]-b[k][0]+temp1;

temp1=0;

}

temp1=0;

for(int j=0;j<NG;j++){

temp1+=n[j][0]*mu[j][0]/(8.3145*T);

}

d_const[l][0]=temp1+nt-getnt(n);

double[][] x=Matrix.AXB(d_coeff,d_const);

del_lnnt=x[l][0];

temp2=0;

for(int j=0;j<NG;j++){

for(int i=0;i<l;i++){

temp2+=A[i][j]*x[i][0];

}

del_lnnm[j][0]=temp2+x[l][0]-mu[j][0]/(8.3145*T);

temp2=0;

}

for(int i=0;i<del_lnnm.length;i++){

lnnm[i][0]=Math.log(n[i][0]);

del_nm[i][0]=Math.exp(del_lnnm[i][0]);

}

///////////////////////////////////////////////////////////////////////////////////////////////////

double q=0;

double max=0;

double min=1e10;

double s=0;

for(int i=0;i<NG;i++){

if((lnnm[i][0]-Math.log(getnt(n)))>-SIZE){

max= Math.abs(del_lnnm[i][0])>Math.abs(max) ? del_lnnm[i][0] :max ;

}

else {

s=del_lnnm[i][0]>0 ? (Math.abs((-1*(lnnm[i][0]-Math.log(getnt(n)))-9.2103404)/(del_lnnm[i][0]-del_lnnt))) : 1000;

min= s>min ? min : s;

}

}

q=(5*Math.abs(del_lnnt)>Math.abs(max)) ? (5*Math.abs(del_lnnt)):Math.abs(max);

//System.out.println("q= "+q);

lambda1=2/q;

lambda2=min;

//System.out.println("lambda1= "+lambda1+" lambda2= "+lambda2);

lambda= (lambda1<lambda2) ? (1<lambda1 ? 1 : lambda1) : (1<lambda2 ? 1 : lambda2);

G=getG(n);

for(int i=0;i<NG;i++){

lnnm[i][0]+=lambda*del_lnnm[i][0];

n[i][0]=Math.exp(lnnm[i][0]);

}

lnnt+=lambda*del_lnnt;

nt=Math.exp(lnnt);

//System.out.println("\nGtot= "+getG(n));

Gnew=getG(n);

etest=etest();

//}

//////////////////////////////////////////////////////////////////////////////////////////////////

it_counter++;

}

}

public double delQ(){

double Q=0;

double href=0;

for(int i=0;i<n.length;i++){

//System.out.println(Te[i]);

Q+=gs[i].ht(T0)*n[i][0]-gs[i].ht(Te[i])*n0[i][0]; }

return Q;//Kj

}

public double delQ_T(double innerT){

double Q=0;

double href=0;

setT(innerT);

setNmax(500);

getEq();

for(int i=0;i<n.length;i++){

Q+=gs[i].ht(innerT)*n[i][0]-gs[i].ht(Te[i])*n0[i][0];

}

setTDefault();

setNmaxDefault();

return Q;//Kj

}

////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

public double Airad(double iQ,double ix1,double ix2){

for(int i=0;i<gs.length;i++){

//System.out.println("LK[i].Formula= "+LK[i].Formula);

if(gs[i].Formula.equals("O2")){

o2 = i;

break;

}

//System.out.println("o2= "+o2);

}

for(int i=0;i<gs.length;i++){

//System.out.println("LK[i].Formula= "+LK[i].Formula);

if(gs[i].Formula.equals("N2")){

n2 = i;

break;

}

}

if(o2!=-1 && n2!=-1){

//Ridder Metodu ile lineer olmayan denklemlerin köklerinin bulunmas?

//referans : Numerical Recipes in C, second edition, William H. Press,

//Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery

//cambridge university press

double[][] x_bracket=new double[2][1];

x_bracket=delQAirBracket(iQ,ix1,ix2);

double x1=x_bracket[0][0];

double x2=x_bracket[1][0];

//System.out.println("x1= "+x1+" x2= "+x2);

int MAXIT=50;

double xacc=1.0e-4;int j;

double fl,fh,xl,xh,swap,dx,del,ff;

double rtf=x1;

fl=delQAir(x1)-iQ;

fh=delQAir(x2)-iQ;

//System.out.println("fl= "+fl+" fh= "+fh);

if (fl*fh > 0.0)System.out.println("Kök s?n?rlar? do?ru olarak seçilmemi? \n sonuç hatal? olabilir");

if (fl < 0.0) {

xl=x1;

xh=x2;

} else {

xl=x2;

xh=x1;

swap=fl;

fl=fh;

fh=swap;

}

dx=xh-xl;

for (j=1;j<=MAXIT;j++) {

rtf=xl+dx*fl/(fl-fh);

ff=delQAir(rtf)-iQ;

if (ff < 0.0) {

del=xl-rtf;

xl=rtf;

fl=ff;

} else {

del=xh-rtf;

xh=rtf;

fh=ff;

}

//System.out.println("rtf= "+rtf);

dx=xh-xl;

//System.out.println("xl= "+xl+" xh= "+xh);

//System.out.println("fl= "+fl+" fh= "+fh);

if (Math.abs(del) < xacc || ff == 0.0) return rtf;

}

System.out.println("Uyarı maximum iterasyon sayısı aşıldı \n"+

" çözüm geçerli olmıyabilir");

return rtf;

}else {

System.out.println("Girdiğiniz karışım O2 ve N2 içermelidir !");

System.exit(1);

}

return 0;

}

public double delQAir(double x){

for(int i=0;i<n0.length;i++) n0[i][0]=n00[i][0];

n0[o2][0]=x;

n0[n2][0]=x*79/21;

System.out.println("T= "+T);

return delQ_T(T);

}

public double delQAir(double x,int ii,int ij){

for(int i=0;i<n0.length;i++){

//System.out.println("n00=\n"+Matrix.toString(n00));

n0[i][0]=n00[i][0];

}

n0[ii][0]=x;

n0[ij][0]=x*79/21;

//System.out.println("n0=\n");

//for(int i=0;i<n0.length;i++) System.out.println(LK[i].Formula+" "+n0[i][0]);

return delQ_T(T);

}

public double[][] delQAirBracket(double iQ,double x1,double x2){

// koklerin yer aldığı alt bölgeleri saptar

// n : verilen bölgeyi böldüğümüz alt bölge sayısı

// x1,x2 : sınır değerleri

// nbb = aranan bölgedeki köksayısı

int n=4;

int nbb=1;

int nb;

int i;

double x,fp,fc,dx;

double xb[][]=new double[2][nbb];

nb=0;

dx=(x2-x1)/n;

x=x1;

//System.out.println("x= "+x);

fp=delQAir(x1)-iQ;

//System.out.println("x1= "+x1+" fp= "+fp);

for (i=1;i<=n;i++)

{

x+=dx;

fc=delQAir(x)-iQ;

//System.out.println("x= "+x+" fc= "+fc);

// eğer kök olan bölge bulunduysa.....

if (fc*fp < 0.0 || fp==0) {

xb[0][nb]=x-dx;

xb[1][nb]=x;

nb++;

}

fp=fc;

if (nbb == nb) return xb;

}

if( nb == 0)

System.out.println("arama tamamlandı kök olan bölge bulunamadı");

else if(nb<nbb){

System.out.println("arama tamamland? sadece "+nb+" adet kök bulundu \n"+

"siz "+nbb+" adet kök için arama yapt?rd?n?z");

double xc[][]=new double[2][nb];

for (i=0;i<nb;i++) {xc[0][i]=xb[0][i];xc[1][i]=xb[1][i];}

return xc;

}

return xb;

}

//////////////////////////////////////////////////////////////////////////////////////////////////////////////

public double[][] TadBracket(double iQ){

// koklerin yer ald??? alt bölgeleri saptar

// n : verilen bölgeyi böldü?ümüz alt bölge say?s?

// x1,x2 : s?n?r de?erleri

// nbb = aranan bölgedeki köksayısı

int n=4;

int nbb=1;

int nb;

double x1=298;

double x2=5000;

int i;

double x,fp,fc,dx;

double xb[][]=new double[2][nbb];

nb=0;

dx=(x2-x1)/n;

x=x1;

fp=delQ_T(x1)-iQ;

//System.out.println("x1= "+x1+" fp= "+fp);

for (i=1;i<=n;i++)

{

x+=dx;

fc=delQ_T(x)-iQ;

//System.out.println("x= "+x+" fc= "+fc);

// eger kök olan bölge bulunduysa.....

if (fc*fp < 0.0 || fp==0) {

xb[0][nb]=x-dx;

xb[1][nb]=x;

nb++;

}

fp=fc;

if (nbb == nb) return xb;

}

if( nb == 0)

System.out.println("arama tamamlandı kök olan bölge bulunamadı");

else if(nb<nbb){

System.out.println("arama tamamlandı sadece "+nb+" adet kök bulundu \n"+

"siz "+nbb+" adet kök için arama yaptırdınız");

double xc[][]=new double[2][nb];

for (i=0;i<nb;i++) {xc[0][i]=xb[0][i];xc[1][i]=xb[1][i];}

return xc;

}

return xb;

}

public double Tad(double iQ)

{

// Ridder Metodu ile lineer olmayan denklemlerin köklerinin bulunmas?

//referans : Numerical Recipes in C, second edition, William H. Press,

//Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery

//cambridge university press

double[][] x_bracket=new double[2][1];

x_bracket=TadBracket(iQ);

double x1=x_bracket[0][0];

double x2=x_bracket[1][0];

//System.out.println("x1= "+x1+" x2= "+x2);

int MAXIT=50;

double xacc=1.0e-4;int j;

double fl,fh,xl,xh,swap,dx,del,ff;

double rtf=x1;

fl=delQ_T(x1)-iQ;

fh=delQ_T(x2)-iQ;

//System.out.println("fl= "+fl+" fh= "+fh);

if (fl*fh > 0.0)System.out.println("Kök s?n?rlar? do?ru olarak seçilmemi? \n sonuç hatal? olabilir");

if (fl < 0.0) {

xl=x1;

xh=x2;

} else {

xl=x2;

xh=x1;

swap=fl;

fl=fh;

fh=swap;

}

//System.out.println("xl= "+xl+" xh= "+xh);

//System.out.println("fl= "+fl+" fh= "+fh);

dx=xh-xl;

for (j=1;j<=MAXIT;j++) {

rtf=xl+dx*fl/(fl-fh);

ff=delQ_T(rtf)-iQ;

if (ff < 0.0) {

del=xl-rtf;

xl=rtf;

fl=ff;

} else {

del=xh-rtf;

xh=rtf;

fh=ff;

}

//System.out.println("rtf= "+rtf);

dx=xh-xl;

//System.out.println("xl= "+xl+" xh= "+xh);

//System.out.println("fl= "+fl+" fh= "+fh);

//System.out.println("n=\n"+Matrix.toString(n));

if (Math.abs(del) < xacc || ff == 0.0) return rtf;

}

System.out.println("Uyarı maximum iterasyon sayısı aşıldı \n"+

" çözüm geçerli olm?yabilir");

return rtf;

}

public void calMu(double[][] in){

for(int i=0;i<mu.length;i++){

mu[i][0]=gs[i].mu(T,P,in[i][0],getnt(in));

}

}

public double[][] getb(double[][] in){

//System.out.println("A= \n"+Matrix.toString(A));

//System.out.println("in= \n"+Matrix.toString(in));

double inner_b[][]=new double[A.length][1];

for(int ii=0;ii<inner_b.length;ii++){

inner_b[ii][0]=0;

for(int ij=0;ij<NG;ij++){

//System.out.println("A[ii][ij]= "+A[ii][ij]+" n0[ij][0]="+n0[ij][0] );

inner_b[ii][0]+=A[ii][ij]*in[ij][0];

}

}

return inner_b;

}

public double etest(){

double[][] e=new double[NG+2][1];

double inner_etest=0;

//System.out.println("n=\n "+Matrix.toString(n));

//System.out.println("deln=\n "+Matrix.toString(del_lnnm));

for(int j=0;j<NG;j++){

//System.out.println(""+del_lnnm[j][0]+" "+n[j][0]+" "+getnt(n));

e[j][0]=n[j][0]*Math.abs(del_lnnm[j][0])/getnt(n);

//System.out.println(j+". eleman "+e[j][0]);

}

e[NG][0]=nt*Math.abs(del_lnnt)/getnt(n);

//System.out.println("toplam n. eleman "+e[NG][0]);

e[NG+1][0]=Math.abs(G-Gnew)/Math.abs(G);

double etest1=Matrix.normEns(Matrix.substract(b0,getb(n)));

double etest0=Matrix.normEns(e);

if(etest0>1e-5){

if(etest1>1e-6){

inner_etest= etest1<etest0 ? etest0 : etest1;

return inner_etest;

}

else return etest0;

}

else{

if(etest1>1e-6) return etest1;

else{

inner_etest= etest1<etest0 ? etest0 : etest1;

return inner_etest;

}

}

//return etest1;

}

public double getnt(double[][] jn){

double nt_inner=0;

for(int i=0;i<jn.length;i++) nt_inner+=jn[i][0];

return nt_inner;

}

public double getG(double[][] in){

calMu(in);

double munt=0;

for(int j=0;j<mu.length;j++) mu[j][0]*=in[j][0];

for(int i=0;i<mu.length;i++) munt+=mu[i][0];

return munt;

}

public double[][] getSolution(){

return n;

}

public int geto2Index(){

return o2;

}

public int getn2Index(){

return n2;

}

}

Program 6.3.1 gibbsSpecies.java

import java.io.*;

public class gibbsSpecies

{ int indicator=-1;

Gas g1;

double P0=1.0;//bar

double T=298.2;

double P=1;

double mu0=0;

Atom[] atomList;

String Formula;

public gibbsSpecies(String SpeciesName,String SpeciesPhase){

if(SpeciesPhase.equals("gas") || SpeciesPhase.equals("(g)") || SpeciesPhase.equals("g") ){

Gas g=new Gas();

String[] b=g.readAllGasNames();

for(int i=0;i<b.length;i++){

if(SpeciesName.equals(b[i])){

indicator=2;

g1=new Gas(SpeciesName);

atomList=g1.atomList;

Formula=g1.gasName.toUpperCase();

}

}

}

else if(SpeciesPhase.equals("liquid") || SpeciesPhase.equals("(l)") || SpeciesPhase.equals("l") ){

System.out.println("For the moment Liquid phase properties are not in use");

}

else if(SpeciesPhase.equals("solid") || SpeciesPhase.equals("(s)") || SpeciesPhase.equals("s") ){

System.out.println("For the moment Solid phase properties are not in use");

}

else if(SpeciesPhase.equals("aqueous") || SpeciesPhase.equals("(aq)") || SpeciesPhase.equals("aq") ){

System.out.println("For the moment Aqueous phase properties are not in use");

}

else System.out.println("finished");

}

public void setP0(double iP){

P0=iP;

}

public double mu(double iT,double iP,double n,double nt){

double mu=0;

if(indicator==1 || indicator==2){

double value=0;

double lnP=Math.log(iP);

value=Math.abs(n)<1e-20? 0 :Math.log(n/nt);

mu=(g1.gt(iT)+8.3145*iT*value+8.3145*iT*lnP);

}

return mu;

}

public void getmu0(double iT,double iP){

mu0=g1.gt(iT);

}

public double ht(double iT){

return g1.ht(iT);

}

}

We can check some of the previously investigated problems by using Gibbs free energy minimisation:

One kmol of CO an done kmol of O₂ established an equilibrium at 3000 K.

Program 6.3.3 example gibbs free energy inimisation by using gibbs class

public class gibbstest3 {

public static void main(String[] arg){

String iLK[]={ "co","o2","co2"};

double[] n0={1,1,0};

double Te[]={3000,3000,3000};

double T1=3000;

double P1=1.01325;

int nmax1=500;//iterasyon sayısı

System.out.println("---------------------------------");

gibbs g1=new gibbs(iLK,n0,Te,T1,P1,nmax1);

g1.getEq();

for(int i=0;i<g1.n.length;i++) System.out.println(g1.gs[i].Formula+" "+g1.n[i][0]);

System.out.println("Q= "+g1.delQ());

System.out.println("A= \n"+Matrix.toString(g1.A));

System.out.println("b= \n"+Matrix.toString(g1.b0));

System.out.println("---------------------------------");

}

}

---------- Capture Output ----------

> "C:\java\bin\javaw.exe" gibbstest3

---------------------------------

CO 0.3336866135142944

O2 0.6668433067571505

CO2 0.6663133864857074

Q = -181692.07676724726

A = 1.000000000000000 0.000000000000000 1.000000000000000

1.000000000000000 2.000000000000000 2.000000000000000

b= 1.000000000000000

3.000000000000000

---------------------------------

> Terminated with exit code 0.

As addition to previous programs, gibbs can be able to calculate adiabatic flame temperatures of an equilibrium state as well.

Program 6.3.4 example gibbs free energy inimisation by using gibbs class

public class gibbstest2 {

public static void main(String[] arg)

{

String s0[]={ "co","h2o","co2","h2","o2" };

double[] n0={1,1,0,0,0};

double Te[]={2500,2500,2500,2500,2500};

double T1=2500;//degree K

double P1=1.01325;//bar

int nmax1=500;//iterasyon sayısı

System.out.println("---------------------------------");

gibbs g1=new gibbs(s0,n0,Te,T1,P1);

g1.getEq();

for(int i=0;i<g1.n.length;i++) System.out.println(g1.gs[i].Formula+" "+g1.n[i][0]);

System.out.println("---------------------------------");

System.out.println("Q= "+g1.delQ());

T1=g1.set_Q(s0,n0,Te,0.0,P1);

System.out.println("T1="+T1);

g1.getEq();

for(int i=0;i<g1.n.length;i++) System.out.println(g1.gs[i].Formula+" "+g1.n[i][0]);

System.out.println("---------------------------------");

}

}

---------- Capture Output ----------

> "C:\java\bin\javaw.exe" gibbstest2

---------------------------------

CO 0.7091934909063149

H2O 0.7083603316367073

CO2 0.2908065090936887

H2 0.29163966836329364

O2 4.1657963479952635E-4

---------------------------------

Q= -6442.059798113942

//adiabatic flame temperature

T1=2566.515550936884

CO 0.7124848532408645

H2O 0.7108823034004179

CO2 0.28751514675913026

H2 0.2891176965995817

O2 8.012749202241687E-4

---------------------------------

Q= -8.02592279427472E-5

> Terminated with exit code 0.

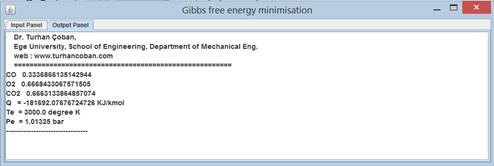
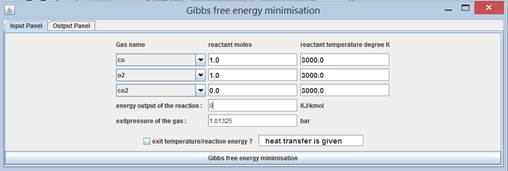
A graphic user interface (GUI) is prepared for gibbs class utilisation

Program 6.3.5 example gibbs free energy minimisation Graphic user interface gibbsTableEN using gibbs class

//======================================================

// Termodinamics-Numerical Analysis package

// Gibbs free energy minimisation

// Dr. Turhan Coban

// Ege University, School of Engineering, Department of Mechanical Eng.

// web : www.turhancoban.com

// =====================================================

import java.lang.Integer;

import java.awt.*;

import java.awt.event.*;

import java.awt.font.*;

import java.awt.geom.*;

import java.awt.image.*;

import javax.swing.*;

import java.util.Locale;

import java.text.*;

import java.io.*;

import java.awt.*;

import java.awt.event.*;

import java.util.*;

import javax.swing.table.*;

public class gibbsTableEN extends JApplet implements ActionListener,ItemListener

{ private static final long serialVersionUID = 37259887589L;

String state[]={" product temperature is given "," heat transfer is given "};

String g1[]={"co","o2","co2"};

double gn1[]={1.0,1.0,0.0};

double gT[]={3000.0,3000.0,3000.0};

double Te=3000.0;

double Pe=1.01325;

double Qe=0;

JPanel panel[];

JTextArea output;

gibbs gib;

JButton b1;

girdiP3EN gp3;

boolean caseT=true;

JCheckBox hhv;

JTextField hhv_lhv;

public String setArea()

{

String s="";

s+=" Dr. Turhan Çoban, \n";

s+=" Ege University, School of Engineering, Department of Mechanical Eng.\n";

s+=" web : www.turhancoban.com\n";

s+=" =======================================================\n";

for(int i=0;i<gib.n.length;i++) s+=gib.gs[i].Formula+" "+gib.n[i][0]+"\n";

Qe=gib.delQ();

s+="Q = "+Qe+" KJ/kmol\n";

s+="Te = "+Te+" degree K\n";

s+="Pe = "+Pe+" bar\n";

s+="---------------------------------";

return s;

}

public void init()

{

//ilk değerler

gp3=new girdiP3EN(g1,gn1,gT,Te,Pe,"Gibbs free energy minimisation");

gib=new gibbs(g1,gn1,gT,Te,Pe);

gib.getEq();

Qe=gib.delQ();

hhv=new JCheckBox("exit temperature/reaction energy ? ",true);

hhv.addItemListener(this);

hhv_lhv=new JTextField(state[0]);

hhv_lhv.setFont(new Font("TimesRoman",Font.BOLD,14));

panel=new JPanel[2];

panel[1]= new JPanel(new FlowLayout());

panel[1].add(hhv);

panel[1].add(hhv_lhv);

JTabbedPane jtp=new JTabbedPane();

b1=new JButton("Gibbs free energy minimisation");

b1.addActionListener(this);

panel[0]= new JPanel(new BorderLayout());

output=new JTextArea(setArea());

output.setFont(new Font("TimesRoman",Font.BOLD,14));

panel[0].add(gp3,BorderLayout.NORTH);

panel[0].add(panel[1],BorderLayout.CENTER);

panel[0].add(b1,BorderLayout.SOUTH);

//b1.addActionListener(this);

JScrollPane skrolPane=new JScrollPane(panel[0]);

jtp.addTab("Input Panel",skrolPane);

jtp.addTab("Output Panel",new JScrollPane(output));

add(jtp);

}

public void actionPerformed(ActionEvent e)

{

if (e.getSource()==b1)

{

g1=gp3.gas;

gn1=gp3.ngas;

gT=gp3.Tgas;

Pe=gp3.Pegas;

if(caseT)

{ Te=gp3.Tegas;

gib.setgibbs(g1,gn1,gT,Te,Pe);

gib.getEq();

Qe=gib.delQ();

}

else

{ Qe=Double.parseDouble(gp3.t2[gp3.n].getText());

Te=gib.set_Q(g1,gn1,gT,Qe,Pe);

gib.getEq();

}

}

else if (e.getSource()==gp3.t2[gp3.n])

{

g1=gp3.gas;

gn1=gp3.ngas;

gT=gp3.Tgas;

Pe=gp3.Pegas;

if(caseT)

{Te=Double.parseDouble(gp3.t2[gp3.n].getText());

gib.setgibbs(g1,gn1,gT,Te,Pe);

gib.getEq();

Qe=gib.delQ();

}

else

{ Qe=Double.parseDouble(gp3.t2[gp3.n].getText());

Te=gib.set_Q(g1,gn1,gT,Qe,Pe);

gib.getEq();

}

}

output.setText(setArea());

repaint();

}

public void itemStateChanged(ItemEvent e)

{ if(e.getSource()==hhv)

{ if(e.getStateChange()==ItemEvent.SELECTED)

{caseT=true;

hhv_lhv.setText(state[0]);

gp3.jl[3].setText("Exit temperature of the gas : ");

gp3.jl[4].setText("degree K ");

g1=gp3.gas;

gn1=gp3.ngas;

gT=gp3.Tgas;

Te=gp3.Tegas;

Pe=gp3.Pegas;

gib.setgibbs(g1,gn1,gT,Te,Pe);

gib.getEq();

output.setText(setArea());

}

else

{caseT=false;

hhv_lhv.setText(state[1]);

gp3.jl[3].setText("energy output of the reaction : ");

gp3.jl[4].setText("KJ/kmol ");

g1=gp3.gas;

gn1=gp3.ngas;

gT=gp3.Tgas;

Qe=gp3.Tegas;

Pe=gp3.Pegas;

Te=gib.set_Q(g1,gn1,gT,Qe,Pe);

gib.getEq();

output.setText(setArea());

}

}

repaint();

}

public static void main(String s[])

{

//main program

JFrame f = new JFrame("Gibbs free energy minimisation");

f.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );

JApplet applet = new gibbsTableEN();

f.getContentPane().add("Center", applet);

applet.init();

f.pack();

f.setSize(new Dimension(1000,600));

f.setVisible(true);

}

}

Program 6.3.6 example gibbs free energy minization Graphic user interface gibbsTableEN using gibbs class, input-output screen program girdiP3EN

import java.lang.Integer;

import java.awt.*;

import java.awt.event.*;

import java.awt.font.*;

import java.awt.geom.*;

import java.awt.image.*;

import javax.swing.*;

import java.util.Locale;

import java.text.*;

import java.io.*;

import java.awt.*;

import java.awt.event.*;

import java.util.*;

import javax.swing.table.*;

public class girdiP3EN extends JPanel implements ActionListener,ItemListener,Serializable

{ private static final long serialVersionUID = 80948739856L;

String gas[];

double ngas[];

double Tgas[];

double Tegas;

double Pegas;

int n1;

JPanel p1,p2,p3,p4,p;

JLabel l1[]; // Label prompt unit

JLabel l2[]; // Label prompt unit

JTextField t1[];

JComboBox<String> c2[];

JTextField t2[];

JTextField t3[];

JLabel jl[];

double a[];

JLabel heading;

int n;

public girdiP3EN(String g1[],double gn1[],double gT1[],double Tegasi,double Pegasi,String hh)

{

Gas1 g=new Gas1("ch4");

gas=new String[g1.length];

ngas=new double[gn1.length];

Tgas=new double[gn1.length];

Tegas=Tegasi;

Pegas=Pegasi;

n1=g1.length;

String baslik[]={"Gas name","reactant moles","reactant temperature degree K"};

jl=new JLabel[7];

jl[0]=new JLabel(baslik[0]);

jl[1]=new JLabel(baslik[1]);

jl[2]=new JLabel(baslik[2]);

jl[3]=new JLabel("exit temperature of the gas : ");

jl[4]=new JLabel("degree K ");

jl[5]=new JLabel("exitpressure of the gas : ");

jl[6]=new JLabel("bar ");

StringTokenizer token=new StringTokenizer(g.readGasNames());

String st[]=new String[token.countTokens()];

int i=0;

while(token.hasMoreTokens())

{

st[i++]=new String(token.nextToken());

}

n=g1.length;

l1=new JLabel[n];

l2=new JLabel[n];

t1=new JTextField[n+2];

a=new double[n];

heading=new JLabel(hh);

p1=new JPanel();

p2=new JPanel();

p3=new JPanel();

p4=new JPanel();

p4.setLayout(new GridLayout(n+3,3,5,5));

c2=new JComboBox[n];

t2=new JTextField[n+2];

t3=new JTextField[n];

p4.add(jl[0]);

p4.add(jl[1]);

p4.add(jl[2]);

for(int iz=0;iz<n1;iz++)

{ gas[iz]=g1[iz];

ngas[iz]=gn1[iz];

Tgas[iz]=gT1[iz];

c2[iz]=new JComboBox<String>(st);

t2[iz]=new JTextField(ngas[iz]+" ");

t3[iz]=new JTextField(Tgas[iz]+" ");

t2[iz].setFont(new Font("TimesRoman",Font.BOLD,14));

t3[iz].setFont(new Font("TimesRoman",Font.BOLD,14));

c2[iz].setSelectedItem(gas[iz]);

t2[iz].addActionListener(this);

p4.add(c2[iz]);

p4.add(t2[iz]);

p4.add(t3[iz]);

c2[iz].addItemListener(this);

t2[iz].addActionListener(this);

t3[iz].addActionListener(this);

}

t2[n]=new JTextField(Tegas+" ");

t2[n+1]=new JTextField(Pegas+" ");

p4.add(jl[3]);

p4.add(t2[n]);

p4.add(jl[4]);

p4.add(jl[5]);

p4.add(t2[n+1]);

p4.add(jl[6]);

t2[n].addActionListener(this);

t2[n+1].addActionListener(this);

p=new JPanel()

{ private static final long serialVersionUID =68476357L;

public Dimension getPrefferedSize()

{

Dimension size=super.getPreferredSize();

size.width=200;

size.height=100;

return size;

}

};

p.add(p4,BorderLayout.NORTH);

add(p);

}

public void actionPerformed( ActionEvent e)

{

int i=0;

for(i=0;i<n;i++)

{ if(e.getSource()==t2[i])

{ ngas[i]=Double.parseDouble(t2[i].getText());

break;

}

else if(e.getSource()==t3[i])

{ Tgas[i]=Double.parseDouble(t3[i].getText());

break;

}

}

if(e.getSource()==t2[n])

{ Tegas=Double.parseDouble(t2[n].getText());

}

else if(e.getSource()==t2[n+1])

{ Pegas=Double.parseDouble(t2[n+1].getText());}

repaint();

}

public void itemStateChanged(ItemEvent ev)

{

for(int i=0;i<n1;i++)

{ if(ev.getSource()==c2[i])

{ gas[i]=(String)c2[i].getSelectedItem();break;}

}

}

public double[] readNgas()

{return ngas;}

public double[] readTgas()

{return ngas;}

public String[] readgas()

{return gas;}

}

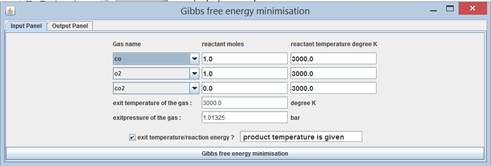
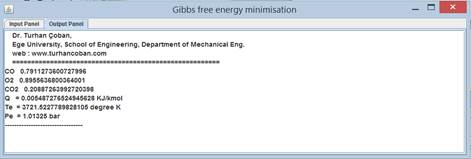
As it is seen from the output at T=3721 K, the reaction reached to adiabatic flame temperature (Total heat transfer is zero)

As a second method, system of equation in the form of

(6.3.14) and

(6.3.15)

terms are very big compare to terms. This makes solution of the nonlinear system difficult. In order to make the sets easier to solve a normalisation factor can be applied to the set as:

C=10RT

so equations become:

(6.3.8a) and (6.3-17)

can now be directly solved by using nonlinear system of equations methods. Equations are formed as a function in f_gibbs class and solved by using continuity(homotophy) method.

Program 6.3.7 interface ifi_xj

@FunctionalInterface

interface ifi_xj

{

// multifunction multi independent variable

// vector of dependent variables are returned

// example f[0]=x[0]+sin(x[1])

// f[1]=x[0]*x[1]-x[1]

// func(x) returns the value of f[0] and f[1]

// as a two dimensional vector

public double[] func(double x[]);

default double[] xp(double x[],double j,double m,double h)

{

//h = dx

//j=-4..4 multiplication factor

//m derivative taken value

int k=x.length;

double xx[]=new double[k];

for(int i=0;i<k;i++)

{ if(i==m) xx[i]=x[i]+j*h;

else xx[i]=x[i];

}

return xx;

}

default double[][] dfunc(double x[])

{

double h=1.0e-12;

return dfunc(x,1,h);

}

default double[][] dfunc(double x[],int n)

{

double h=1.0e-12;

return dfunc(x,n,h);

}

default double[][] dfunc(double x[],int n,double h)

{

int k=x.length; //number of x values (dimension)

double df[][]=new double[k][k];

for(int i=0;i<k;i++)

{ for(int j=0;j<k;j++)

{df[i][j]=dfunc(x,n,i,j,h);}

}

return df;

}

default double dfunc(double x[],int n,int j,int m)

{

double h=1.0e-12;

return dfunc(x,n,j,m,h);

}

default double dfunc(double x[],int n,int j,int m,double h)

{ // derivative of x[m]

//m derivative taken value

//jth equation

//nth derivative of the equation (n=0) function value

//n=1 first derivative n=2 second derivative..

int k=x.length; //number of x values (dimension)

double hh=1/h;

double ff[][]=new double[9][3];

double xp[][]=new double[9][3];

double df;

int j1;

double x1=0;

x1=x[m];

for(int jj=-4;jj<=4;jj++)

{ j1=jj+4;

xp[j1]=xp(x,jj,m,h);

ff[j1]=func(xp[j1]);

}

if(n==0)

{df=ff[4][j];}

else if(n==1)

{ df=(3.0*ff[0][j]-32.0*ff[1][j]+168.0*ff[2][j]-672.0*ff[3][j]+672.0*ff[5][j]-168.0*ff[6][j]+32.0*ff[7][j]-3.0*ff[8][j])/840.0*hh;}

else if(n==2)

{df=(-14350.0*ff[4][j]-9.0*ff[0][j]+128*ff[1][j]-1008*ff[2][j]+8064*ff[3][j]+8064.0*ff[5][j]-1008.0*ff[6][j]+128.0*ff[7][j]-9.0*ff[8][j])/5040.0*hh*hh;}

else if(n==3)

{df=(-7.0*ff[0][j]+72.0*ff[1][j]-338.0*ff[2][j]+488.0*ff[3][j]-488.0*ff[5][j]+338.0*ff[6][j]-72.0*ff[7][j]+7.0*ff[8][j])/240.0*hh*hh*hh;}

else if(n==4)

{df=(2730.0*ff[4][j]+7.0*ff[0][j]-96.0*ff[1][j]+676.0*ff[2][j]-1952.0*ff[3][j]-1952.0*ff[5][j]+676.0*ff[6][j]-96.0*ff[7][j]+7.0*ff[8][j])/240.0*hh*hh*hh*hh;}

else if(n==5)

{df=(ff[0][j]-9.0*ff[1][j]+26.0*ff[2][j]-29.0*ff[3][j]+29.0*ff[5][j]-26.0*ff[6][j]+9.0*ff[7][j]-ff[8][j])/6.0*hh*hh*hh*hh*hh;}

else if(n==6)

{df=(-150.0*ff[4][j]-ff[0][j]+12.0*ff[1][j]-52.0*ff[2][j]+116.0*ff[3][j]+116.0*ff[5][j]-52.0*ff[6][j]+12.0*ff[7][j]-ff[8][j])/4.0*hh*hh*hh*hh*hh*hh;}

else if(n==7)

{df=(-ff[0][j]+6.0*ff[1][j]-14.0*ff[2][j]+14.0*ff[3][j]-14.0*ff[5][j]+14.0*ff[6][j]-6.0*ff[7][j]+ff[8][j])/2.0*hh*hh*hh*hh*hh*hh*hh;}

else if(n==8)

{df=(70.0*ff[4][j]+ff[0][j]-8.0*ff[1][j]+28.0*ff[2][j]-56.0*ff[3][j]-56.0*ff[5][j]+28.0*ff[6][j]-8.0*ff[7][j]+ff[8][j])*hh*hh*hh*hh*hh*hh*hh*hh;}

else df=0;

return df;

}

}

Program 6.3.8 example gibbs free energy minization , by directly solving non-linear system of equations, f_gibbs general input function

import java.io.*;

import java.util.*;

import javax.swing.*;

import java.awt.*;

import java.awt.event.*;

class if_gibbs implements ifi_xj

{ public double[][] A;

public gibbsSpecies[] gs;

public double[] n0;

public String name[];

double[] n;

double[] del_lnnm;

double[] del_nm;

double[] lnnm;

double nt;

double lnnt;

double del_lnnt;

public double R;

public int NG;//Gas species number

public int l;//element number

double[][] d_coeff;

double[] d_const;

double[] b0;

double[] b;

double[] mu;

double[] mutemp;

double P;

double T;

double T0;

double[] Te;

double etemp=0;

double Tref=298.15;

double G=0;

double Gnew=0;

double diff=0;

double SIZE=25.328436;;

double ntahminilk;

int it_max=100;

int it_max0=100;

int o2=-1;

int n2=-1;

double x1[];

double x2[];

public double C;

public if_gibbs(String igs[],double[] in0,double iTe[],double iT,double iP)

{ R=8.31451;

C=50*R*iT;

Te=new double[iTe.length];

name=new String[iTe.length];

for(int i=0;i<iTe.length;i++)

{Te[i]=iTe[i];name[i]=igs[i];}

setgibbs(igs,in0,iT,iP);

}

public void setgibbs(String igs[],double[] in0,double iT,double iP){

gs=new gibbsSpecies[igs.length];

for(int i=0;i<igs.length;i++){

gs[i]=new gibbsSpecies(igs[i],"gas");

}

int nn=igs.length;

int nat=110;

double B[][]=new double[nat][nn];

int nk=0;

for(int i=0;i<nn;i++){

for(nk=0;nk<gs[i].atomList.length;nk++){

B[gs[i].atomList[nk].number-1][i]=gs[i].atomList[nk].N;

}

}

int natcount=0;

boolean zeroflag[]=new boolean[110];

for(int j=0;j<nat;j++)

{zeroflag[j]=false;for(int i=0;i<nn;i++){if(B[j][i]!=0){zeroflag[j]=true;}};if(zeroflag[j]) natcount++;}

A=new double[natcount][nn];

int k=0;

for(int j=0;j<nat;j++)

{if(zeroflag[j]){A[k]=B[j];k++;}}

n0=in0;

P=iP;

T=iT;

T0=iT;

mu=new double[gs.length];

l=A.length;

NG=A[0].length;

b=new double[l];

nt=getnt(n0);

ntahminilk=nt/n0.length;

n=new double[n0.length];

for(int i=0;i<n0.length;i++){

n[i]=ntahminilk;

}

nt=getnt(n);

b0=new double[l];

for(int ii=0;ii<b0.length;ii++)

{for(int ij=0;ij<NG;ij++)

{ double carpim=A[ii][ij]*n0[ij];

b0[ii]+=carpim;

}

}

calMu(n0);

}

public double getnt(double[] jn)

{

double nt_inner=0;

for(int i=0;i<jn.length;i++) {nt_inner+=jn[i];}

return nt_inner;

}

public void setN0(double[] in0){

for(int i=0;i<n0.length;i++) n0[i]=in0[i];

}

public void setT(double iTeq){

T=iTeq;

calMu(n0);

}

public void setTDefault(){

T=T0;

}

public void calMu(double[] in){

for(int i=0;i<mu.length;i++){

double inT=getnt(in);

mu[i]=gs[i].mu(T,P,in[i],inT);

}

}

public double[] getb(double[] in){

double inner_b[]=new double[A.length];

for(int ii=0;ii<inner_b.length;ii++){

inner_b[ii]=0;

for(int ij=0;ij<NG;ij++){

inner_b[ii]+=A[ii][ij]*in[ij];

}

}

return inner_b;

}

public double A_lambda(double[] in,int j)

{

double inner_b=0;

for(int i=0;i<in.length;i++)

{inner_b+=A[i][j]*in[i];}

return inner_b;

}

public double getG(double[] in)

{

calMu(in);

double munt=0;

for(int j=0;j<mu.length;j++) mu[j]*=in[j];

for(int i=0;i<mu.length;i++) munt+=mu[i];

return munt;

}

public double[] func(double x[])

{

//çözümü istenen fonksiyon

int n1=x.length;

double ff[]=new double[n1];

double G;

double x1[]=new double[NG];

double x2[]=new double[l];

for(int i=0;i<NG;i++) {x1[i]=x[i];//System.out.println("x1["+i+"] = "+x1[i]);

} //n_i

for(int i=NG;i<(NG+l);i++) {x2[i-NG]=x[i];} //lambda_k

calMu(x1);

double f1[]=mu;

double xx=0;

for(int i=0;i<NG;i++) {ff[i]=f1[i];}

for(int j=0;j<NG;j++) {xx=A_lambda(x2,j);ff[j]+=C*xx;}

b=getb(x1);

//System.out.println("b="+Matrix.toString(b)+"b0="+Matrix.toString(b0));

for(int i=NG;i<(NG+l);i++) {ff[i]=b[i-NG]-b0[i-NG];}

return ff;

}

public void equilibrium_print(double ni[])

{ int nn=ni.length;

double x[]=new double[nn];

double x0[]=new double[nn];

double nnt=0;

double nn0t=0;

for(int i=0;i<nn;i++){nnt+=ni[i];nn0t+=n0[i];}

for(int i=0;i<nn;i++){x[i]=ni[i]/nnt;x0[i]=n0[i]/nn0t;}

JTextArea jta;

JPanel jpan=new JPanel();

jpan.setLayout(new BorderLayout());

String s="";

//s+="Treactant = "+TR+" degree K\n";

//s+="Tproduct = "+TP+ " degree K\n";

s+="P = "+P+" bar\n";

s+="==========================================\n";

jta=new JTextArea(s);

String heading[]={"name","n0 mole in","x0 mole ratio in","n mole out","x mole ratio out"};

String s1[][]=new String[nn+1][5];

for(int i=0;i<nn;i++)

{s1[i][0]=name[i];

s1[i][1]=""+n0[i];

s1[i][2]=""+x0[i];

s1[i][3]=""+ni[i];

s1[i][4]=""+x[i];

}

s1[nn][0]="total";

s1[nn][1]=""+nn0t;

s1[nn][2]=""+1;

s1[nn][3]=""+nnt;

s1[nn][4]=""+1;

JTable jt;

genelModel gm=new genelModel(s1,heading);

jt=new JTable(gm);

jpan.add(jta,BorderLayout.NORTH);

jpan.add(new JScrollPane(jt),BorderLayout.SOUTH);

String bb="Equilibrium Chemical Reaction";

JFrame cerceve=new JFrame(bb);

cerceve.addWindowListener(new BasicWindowMonitor());

cerceve.getContentPane().add(new JScrollPane(jpan));

cerceve.pack();

cerceve.setVisible(true);

}

}

Program 6.3.9 example gibbs free energy minization , by directly solving non-linear system of equations, gibbs1i

import java.util.*;

import java.awt.*;

import java.applet.Applet;

import java.awt.event.*;

import javax.swing.*;

//solution of nonlinear system of equations by using continuation method

public class gibbs1i

{ //igs name of species fe "co", "co2" "o2"

//n0 initial species configuration

//Ti initial temperatures

// T0 equilibrium temperature

// Pi pressure

// ni first estimation of equilibrium moles

public static double[] gibbs(String igs[],double n0[],double Ti[],double To,double Pi,double ni[])

{if_gibbs f=new if_gibbs(igs,n0,Ti,To,Pi);

double R=8.3145;

int NG=f.NG;

int l=f.l;

int n1=NG+l;

double n[]=new double[n1];

//initial conditions

for(int i=0;i<NG;i++)

{n[i]=ni[i];}

//solution of non-linear equation

for(int i=NG;i<n1;i++)

{n[i]=200.0/(50.0*R*To);}

//Nonlinear solution method

double [] r1= continuationRK6(f,n,20);

//results...

double r2[]=new double[NG];

for(int i=0;i<NG;i++) {r2[i]=r1[i];}

return r2;

}

public static void equilibrium_print(String name[],double n0[],double ni[],double Ti[],double To,double Pi)

{ int nn=ni.length;

double x[]=new double[nn];

double x0[]=new double[nn];

double nnt=0;

double nn0t=0;

for(int i=0;i<nn;i++){nnt+=ni[i];nn0t+=n0[i];}

for(int i=0;i<nn;i++){x[i]=ni[i]/nnt;x0[i]=n0[i]/nn0t;}

JTextArea jta;

JPanel jpan=new JPanel();

jpan.setLayout(new BorderLayout());

String s="";

s+="==========================================\n";

s+="P = "+Pi+" bar \n";

s+=toString(name,n0,ni);

jta=new JTextArea(s);

String heading[]={"name","Tin","n0 mole in","x0 mole ratio in","Tout","n mole out","x mole ratio out"};

String s1[][]=new String[nn+1][7];

for(int i=0;i<nn;i++)

{s1[i][0]=name[i];

s1[i][1]=""+Ti[i];

s1[i][2]=""+n0[i];

s1[i][3]=""+x0[i];

s1[i][4]=""+To;

s1[i][5]=""+ni[i];

s1[i][6]=""+x[i];

}

s1[nn][0]="total";

s1[nn][1]=" ";

s1[nn][2]=""+nn0t;

s1[nn][3]=""+1;

s1[nn][4]=" ";

s1[nn][5]=""+nnt;

s1[nn][6]=""+1;

JTable jt;

genelModel gm=new genelModel(s1,heading);

jt=new JTable(gm);

jpan.add(jta,BorderLayout.NORTH);

jpan.add(new JScrollPane(jt),BorderLayout.SOUTH);

String bb="Gibbs free energy minimisation";

JFrame cerceve=new JFrame(bb);

cerceve.addWindowListener(new BasicWindowMonitor());

cerceve.getContentPane().add(new JScrollPane(jpan));

cerceve.pack();

cerceve.setVisible(true);

}

public static double[] continuationRK6(ifi_xj f,double x[],int N)

{

//====================================================

// Roots of nonlinear system of equations Homotophy RK6

// yi+1 = yi + (1/90)*( 7k1 + 32k3 +12k4+32k5+7k6)h

// k1=f(xi,yi)

// k2=f(xi+0.25h , yi+0.25k1h)

// k3=f(xi+0.25h , yi+0.125k1h+0.125k2h)

// k4=f(xi+0.5h , yi - 0.5k2h+k3h)

// k5=f(xi+0.75h , yi + (3/16)k1h+(9/16)k4h)

// k6=f(xi+h , yi - (3/7)k1h+(2/7)k2h+(12/7)k3h - (12/7)k4h+(8/7)k5h)

//===================================================

//x vector of independent variables

//y vector of dependent variables

//dy derivative vector of dependent variables

int i;

int nmax=1000;

double tolerance=1.0e-15;

int n=x.length;

double h=1.0/(double)N;

double b[]=new double[n];

double x1[]=new double[n];

double k[][]=new double[6][n];

double A[][]=new double[n][n];

b=multiply(-h,f.func(x));

for(i=0;i<N;i++)

{

A=f.dfunc(x);

// k1=f(xi,yi)

k[0]=multiply(inv(A),b);

x1=add(x,multiply(0.25,k[0]));

A=f.dfunc(x1);

// k2=f(xi+0.25h , yi+0.25k1h)

k[1]=multiply(inv(A),b);

x1=add(x,add(multiply(0.125,k[0]),multiply(0.125,k[1])));

A=f.dfunc(x1);

// k3=f(xi+0.25h , yi+0.125k1h+0.125k2h)

k[2]=multiply(inv(A),b);

x1=add(x,add(multiply(-0.5,k[1]),k[2]));

A=f.dfunc(x1);

// k4=f(xi+0.5h , yi - 0.5k2h+k3h)

k[3]=multiply(inv(A),b);

x1=add(x,add(multiply((3.0/16.0),k[0]),multiply((9.0/16.0),k[3])));

A=f.dfunc(x1);

// k5=f(xi+0.75h , yi + (3/16)k1h+(9/16)k4h)

k[4]=multiply(inv(A),b);

x1=add(x,

add(multiply((-3.0/7.0),k[0]),add(multiply((2.0/7.0),k[1]),

add(multiply((12.0/7.0),k[2]),

add(multiply((-12.0/7.0),k[3]),multiply((8.0/7.0),k[4]))))));

A=f.dfunc(x1);

// k6=f(xi+h , yi - (3/7)k1h+(2/7)k2h+(12/7)k3h - (12/7)k4h+(8/7)k5h)

k[5]=multiply(inv(A),b);

// yi+1 = yi + (1/90)*( 7k1 + 32k3 +12k4+32k5+7k6)h

for(int j=0;j<n;j++) {x[j]=x[j]+1.0/90.0*(7.0*k[0][j]+32.0*k[2][j]+12.0*k[3][j]+32.0*k[4][j]+7.0*k[5][j]);}

}

return x;

}

public static String toString(String name[],double n0[],double n[])

{

// writes chemical reaction in chemistry norm

int nn=n0.length;

String s="";

String gasname;

for(int i=0;i<nn;i++)

{

Gas g=new Gas(name[i]);

if(n0[i]!=0)

{ if(n0[i]!=1.0) s+=""+n0[i];

s+=g.toString();

if(i!=(nn-1)) s+=" + ";

else

{ if(s.endsWith(" + ")) s=s.substring(0,s.length()-2);

s+=" --> ";}

}

else

{ if(s.endsWith(" + ")) s=s.substring(0,s.length()-2);

if(i==(nn-1)) s+=" --> ";

}

}

for(int i=0;i<nn;i++)

{

Gas g=new Gas(name[i]);

if(n[i]!=0)

{ if(n[i]!=1.0) s+=""+n[i];

s+=g.toString();

if(i!=(nn-1)) s+=" + ";

else s+=" ";

}

}

return s;

}

// (Continuity-homotopy) method to solve a system of nonlinear equations

public static double[] multiply(double left,double[] right)

{

//multiplying a vector with a constant

int i;

int n=right.length;

double b[];

b=new double[n];

for(i=0;i<n;i++)

{b[i]=left*right[i];}

return b;

}

public static double[] multiply(double[][] left,double[] right)

{

//multiplication of one matrix with one vector

int ii,jj,i,j,k;

int m1=left[0].length;

int n1=left.length;

int m2=right.length;

double[] b;

b=new double[m2];

if(n1 != m2)

{

System.out.println("inner matrix dimensions must agree");

for(ii=0;ii<n1;ii++)

{

b[ii]=0;

}

return b;

}

for(i=0;i<m1;i++)

{

b[i]=0;

for(k=0;k<n1;k++)

b[i]+=left[i][k]*right[k];

}

return b;

//end of multiply of a matrix and a vector

}

public static double[] add(double[] left,double[] right)

{

//addition of two vectors

int n1=left.length;

int n2=right.length;

int nMax;

int i;

if(n1>=n2) nMax=n1;

else nMax=n2;

double b[];

b=new double[nMax];

for(i=0;i<n1;i++)

{

b[i]=b[i]+left[i];

}

for(i=0;i<n2;i++)

{

b[i]=b[i]+right[i];

}

return b;

//end of vector addition method

}

public static double[][] inv(double[][] a)

{

// INVERSION OF A MATRIX

// inversion by using gaussian elimination

// with full pivoting

int n=a.length;

int m=a[0].length;

double b[][];

b=new double[n][n];

int indxc[];

int indxr[];

double ipiv[];

indxc=new int[n];

indxr=new int[n];

ipiv=new double[n];

int i,j,k,l,ll,ii,jj;

int icol=0;

int irow=0;

double big,dum,pivinv,temp;

if(n!=m)

{ System.out.println("Matrix must be square ");

for(ii=0;ii<n;ii++)

for(jj=0;jj<n;jj++)

b[ii][jj]=0.0;

return b;

}

for(i=0;i<n;i++)

for(j=0;j<n;j++)

b[i][j]=a[i][j];

for(i=0;i<n;i++)

{

big=0.0;

for(j=0;j<n;j++)

{

if(ipiv[j] != 1)

for(k=0;k<n;k++)

{

if(ipiv[k] == 0)

{

if(Math.abs(b[j][k]) >= big)

{

big=Math.abs(b[j][k]);

irow=j;

icol=k;

}

}

else if(ipiv[k] > 1 )

{

System.out.println("error : inverse of the matrix : singular matrix-1");

for(ii=0;ii<n;ii++)

for(jj=0;jj<n;jj++)

b[ii][jj]=0.0;

return b;

}

}

}

++ ipiv[icol];

if(irow != icol)

for(l=0;l<n;l++)

{

temp=b[irow][l];

b[irow][l]=b[icol][l];

b[icol][l]=temp;

}

indxr[i]=irow;

indxc[i]=icol;

if(b[icol][icol] == 0.0)

{

System.out.println("error : inverse of the matrix : singular matrix-2");

for(ii=0;ii<n;ii++)

for(jj=0;jj<n;jj++)

b[ii][jj]=0.0;

return b;

}

pivinv=1.0/b[icol][icol];

b[icol][icol]=1.0;

for(l=0;l<n;l++) b[icol][l] *=pivinv;

for(ll=0;ll<n;ll++)

if(ll != icol)

{

dum=b[ll][icol];

b[ll][icol]=0.0;

for(l=0;l<n;l++) b[ll][l]-= b[icol][l]*dum;

}

}

for(l=n-1;l>=0;l--)

{

if(indxr[l] != indxc[l])

for(k=0;k<n;k++)

{

temp=b[k][indxc[l]];

b[k][indxc[l]]=b[k][indxr[l]];

b[k][indxr[l]]=temp;

}

}

return b;

}

public static void main(String arg[])

{ /*

String iLK[]={ "co","o2","co2" }; //species

double[] n0={1,1,0}; //initial moles of species

double Te[]={298.15,298.15,298.15}; //İnitial temperatures

double T1=3000; //equilibrium temperature

double P1=1.01325; //equilibrium pressure

double ni[]={0.5,0.5,0.5}; //initial estimation for equilibrium species

*/

String iLK[]={ "ch4","o2","n2","co2","h2o","co" };

double[] n0={1,1,2.0*3.76,0,0,0};

double Te[]={298.15,298.15,298.15,298.15,298.15,298.15};

double T1=2500;

double P1=1.01325;

double ni[]={0.5,0.5,0.5,0.5,0.5,0.5}; //initial estimation for equilibrium species

double [] r1= gibbs(iLK,n0,Te,T1,P1,ni);

equilibrium_print(iLK,n0,r1,Te,T1,P1);

}

}

Non linear continuity method listed before as Program 6.2.3 which is using a combination of continuity and Newton-Raphson non-linear system of equation solution methods.

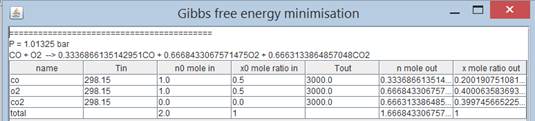
If the temperature drops CO will vanish and reaction wil be converted to a complete combustion

If no additional gases is defined, equilibrium state will find the chemical balance

If additional gases is given in equilibrium, gas combination will drastically change

public static void main(String arg[])

{ String iLK[]={ "ch4","o2","n2","co2","h2o","co" };

double[] n0={1,1,3.76,0,0,0};

double Te[]={298.15,298.15,298.15,298.15,298.15,298.15};

double T1=2500;

double P1=1.01325;

double [] r1= gibbs(iLK,n0,Te,T1,P1);

equilibrium_print(iLK,n0,r1,Te,T1,P1);

}

Gibbs free energy minimisation can also be applied by directly minimizing gibbs function, but since equation is very unstable results may not be obtained by using any optimisation method.

Program 6.3.10 Interface if_xj

@FunctionalInterface

interface if_xj extends iMathd

{

// single function multi independent variable

// a single value is returned indiced to equation_ref

public double func(double x[]);

default double func(double x1,double y1)

{

double x[]=new double[2];

x[0]=x1;

x[1]=y1;

return func(x);

}

default double[] dfunc(double x[])

{int n=x.length;

double c[]=new double[n];

for(int i=0;i<n;i++)

{c[i]=dfunc(x,i);}

return c;

}

default double[][] d2func(double x[])

{int n=x.length;

double c[][]=new double[n][n];

for(int i=0;i<n;i++)

{for(int j=0;j<n;j++)

{ int xref[]={i,j};

c[i][j]=d2func(x,xref);

}

}

return c;

}

default double d2func(double x[],int x_ref[])

{// derivative of the function with respect to x_ref

double h0=0.0256;

int i,m;

int n=7;

double f1,f2;

double x1[];

x1=new double[x.length];

double x2[];

x2=new double[x.length];

for(i=0;i<x.length;i++)

{

x1[i]=x[i];

x2[i]=x[i];

}

//derivative of a simple function

double T[][];

T=new double[n][n];

double h[];

h=new double[n];

//vector<double> h(n,0);

for(i=0;i<n;i++)

{

h[i]=0;

for(int j=0;j<n;j++)

T[i][j]=0;

}

h[0]=h0;

double r=0.5;

for( i=1;i<n;i++)

{

h[i]=h0*Math.pow(r,i);

}

for(i=0;i<n;i++)

{

x1[x_ref[1]]+=h[i];

x2[x_ref[1]]-=h[i];

f1=dfunc(x1,x_ref[0]);

f2=dfunc(x2,x_ref[0]);

T[i][0]=( f1 - f2)/(2.0*h[i]);

x1[x_ref[1]]=x[x_ref[1]];

x2[x_ref[1]]=x[x_ref[1]];

}

for(m=1;m<n;m++)

{

for(i=0;i<n-m;i++)

{

T[i][m]=(h[i]*h[i]*T[i+1][m-1] - h[i+m]*h[i+m]*T[i][m-1])/(h[i]*h[i]

- h[i+m]*h[i+m]);

}

}

double xx=T[0][n-1];

return xx;

}

default double dfunc(double x[],int x_ref)

{ // derivative of the function with respect to x_ref

double h0=0.0256;

int i,m;

int n=7;

double f1,f2;

double x1[];

x1=new double[x.length];

double x2[];

x2=new double[x.length];

for(i=0;i<x.length;i++)

{

x1[i]=x[i];

x2[i]=x[i];

}

//derivative of a simple function

double T[][];

T=new double[n][n];

double h[];

h=new double[n];

//vector<double> h(n,0);

for(i=0;i<n;i++)

{

h[i]=0;

for(int j=0;j<n;j++)

T[i][j]=0;

}

h[0]=h0;

double r=0.5;

for( i=1;i<n;i++)

{

h[i]=h0*Math.pow(r,i);

}

for(i=0;i<n;i++)

{

x1[x_ref]+=h[i];

x2[x_ref]-=h[i];

f1=func(x1);

f2=func(x2);

T[i][0]=( f1 - f2)/(2.0*h[i]);

x1[x_ref]=x[x_ref];

x2[x_ref]=x[x_ref];

}

for(m=1;m<n;m++)

{

for(i=0;i<n-m;i++)

{

T[i][m]=(h[i]*h[i]*T[i+1][m-1] - h[i+m]*h[i+m]*T[i][m-1])/(h[i]*h[i]

- h[i+m]*h[i+m]);

}

}

double xx=T[0][n-1];

return xx;

}}

Program 6.3.11 example gibbs free energy minization , by gibbs equation function if1_gibbs

class if1_gibbs implements if_xj

{ public double[][] A;

public gibbsSpecies[] gs;

public String name[];

public double[] n0;

public double R;

double[] n;

double[] del_lnnm;

double[] del_nm;

double[] lnnm;

double nt;

double lnnt;

double del_lnnt;

public int NG;//Gas species number

public int l;//element number

double[][] d_coeff;

double[] d_const;

double[] b0;

double[] b;

double[] mu;

double[] mutemp;

double P;

double T;

double T0;

double[] Te;

double etemp=0;

double Tref=298.15;

double G=0;

double Gnew=0;

double diff=0;

double SIZE=25.328436;;

double ntahminilk;

int it_max=100;

int it_max0=100;

int o2=-1;

int n2=-1;

double x1[];

double x2[];

double C;

public if1_gibbs(String igs[],double[] in0,double iTe[],double iT,double iP)

{ R=8.3145;

C=50*R*iT;

Te=new double[iTe.length];

name=new String[iTe.length];

for(int i=0;i<iTe.length;i++)

{Te[i]=iTe[i];name[i]=igs[i];}

setgibbs(igs,in0,iT,iP);

}

public void setgibbs(String igs[],double[] in0,double iT,double iP){

gs=new gibbsSpecies[igs.length];

for(int i=0;i<igs.length;i++){

gs[i]=new gibbsSpecies(igs[i],"gas");

}

int nn=igs.length;

int nat=110;

double B[][]=new double[nat][nn];

int nk=0;

for(int i=0;i<nn;i++){

for(nk=0;nk<gs[i].atomList.length;nk++){

B[gs[i].atomList[nk].number-1][i]=gs[i].atomList[nk].N;

}

}

int natcount=0;

boolean zeroflag[]=new boolean[110];

for(int j=0;j<nat;j++)

{zeroflag[j]=false;for(int i=0;i<nn;i++){if(B[j][i]!=0){zeroflag[j]=true;}};if(zeroflag[j]) natcount++;}

A=new double[natcount][nn];

int k=0;

for(int j=0;j<nat;j++)

{if(zeroflag[j]){A[k]=B[j];k++;}}

n0=in0;

P=iP;

T=iT;

T0=iT;

mu=new double[gs.length];

l=A.length;

NG=A[0].length;

b=new double[l];

nt=getnt(n0);

ntahminilk=nt/n0.length;

n=new double[n0.length];

for(int i=0;i<n0.length;i++){

n[i]=ntahminilk;

}

nt=getnt(n);

b0=new double[l];

for(int ii=0;ii<b0.length;ii++)

{for(int ij=0;ij<NG;ij++)

{ double carpim=A[ii][ij]*n0[ij];

b0[ii]+=carpim;

}

}

calMu(n0);

}

public double getnt(double[] jn)

{

double nt_inner=0;

for(int i=0;i<jn.length;i++) {nt_inner+=jn[i];}

return nt_inner;

}

public void setN0(double[] in0){

for(int i=0;i<n0.length;i++) n0[i]=in0[i];

}

public void setT(double iTeq){

T=iTeq;

calMu(n0);

}

public void setTDefault(){

T=T0;

}

public void calMu(double[] in){

for(int i=0;i<mu.length;i++){

double inT=getnt(in);

mu[i]=gs[i].mu(T,P,in[i],inT);

}

}

public double[] getb(double[] in){

double inner_b[]=new double[A.length];

for(int ii=0;ii<inner_b.length;ii++){

inner_b[ii]=0;

for(int ij=0;ij<NG;ij++){

inner_b[ii]+=A[ii][ij]*in[ij];

}

}

return inner_b;

}

public double A_lambda(double[] in,int j)

{

double inner_b=0;

for(int i=0;i<in.length;i++)

{inner_b+=A[i][j]*in[i];}

return inner_b;

}

public double getG(double[] in)

{

calMu(in);

double munt=0;

for(int j=0;j<mu.length;j++) mu[j]*=in[j];

for(int i=0;i<mu.length;i++) munt+=mu[i];

return munt;

}

public double func(double x[])

{

double ff1=0;

int n1=x.length;

double ff[]=new double[n1];

double G;

double x1[]=new double[NG];

double x2[]=new double[l];

for(int i=0;i<NG;i++)

{x1[i]=x[i];}

for(int i=NG;i<(NG+l);i++) {x2[i-NG]=x[i];}

calMu(x1);

for(int i=0;i<NG;i++) {ff1+=mu[i]*x1[i];}

b=getb(x1);

for(int i=0;i<l;i++) {ff1+=C*x2[i]*(b[i]-b0[i]);}

return ff1;

}

}

Example program minimizing gibbs freee energy equation by using continuity and Newton-Raphson method.

Program 6.3.12 example gibbs free energy minization , by gibbs equation function f1_gibbstest

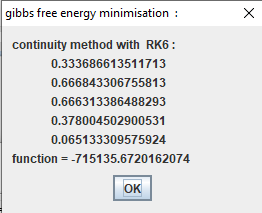
import java.util.*;

import java.awt.*;

import java.applet.Applet;

import java.awt.event.*;

import javax.swing.*;

public class if1_gibbstest

{

public static void main(String arg[])

{ String iLK[]={ "co","o2","co2" };

double[] n0={1,1,0};

double Te[]={298.15,298.15,298.15};

double T1=3000;

double R=8.3145;

double C=10*R*T1;

double xx=10000.0/C;

double P1=1.01325;

double [] x0={0.5,0.5,0.5,xx,xx};

if1_gibbs f=new if1_gibbs(iLK,n0,Te,T1,P1);

double [] r= NA34F.newton_continuationRK4(f,x0,10);

String s="continuity method with RK6 : \n"+Matrix.toStringT(r)+"function = "+f.func(r)+"\n";

String s1="gibbs free energy minimisation : ";

JOptionPane.showMessageDialog(null,s,s1,JOptionPane.PLAIN_MESSAGE);

}

}

PROBLEMS

PROBLEM 1: The following reaction is given: Temperature of reactants is T=300 K

a) Calculate equilibrium of gases when outside temperature is T=1200 K

b) Calculate equilibrium of gases when outside temperature is T=2000 K

c) Calculate equilibrium of gases when outside temperature is T=3000 K

d) Calculate equilibrium of gases when outside temperature is at adiabatic flame temperature (Q=0)

You can use gibbs.java, gibstest2.java, gibstest3.java, gibsTableEN.java. apply Gibbs free energy minimisation method

PROBLEM 2: Repeat the same problem, but this time use equilibrium equations

a) Calculate equilibrium of gases when outside temperature is T=1200 K

b) Calculate equilibrium of gases when outside temperature is T=2000 K

c) Calculate equilibrium of gases when outside temperature is T=3000 K