NEMLİ HAVANIN  TERMODİNAMİK ÖZELLİKLERİNİN VE YAŞ HAVA PROSESLERİNİN MODELLENMESİ

 

M. Turhan Çoban, Halil Atalay

Ege Üniversitesi Mühendislik Fakültesi

Makine Mühendisliği Bölümü

 

                                                                                                 Özet:

Su buharının termodinamik özelliklerini irdeleyen steam.java programı, ideal gazların termodinamik özelliklerini hesaplayan idealgaz.java programı, bu iki programı kullanarak yaş havanın termodinamik özelliklerini hesaplayan yashava.java programı ve yashava. java programından yola çıkılarak yashavaprosesleri. java   programı  geliştirilmiştir. Bu programların oluşturulmasında kullanılan temel denklemler, programların oluşturulması ve kullanılmasına dair temel bilgiler bu çalışmada sunulmuştur.

 

Anahtar Kelimeler: psikometri, nemli hava, ısıtma havalandırma, enerji, su buharı, yaş hava prosesleri.

 

1.Giriş:

Günümüzde enerji sistemlerinin analizlerinde bilgisayar sistemlerinden yoğun olarak faydalanılmaktadır. Enerji sistemlerinin en temel özellikleri gazların termodinamik ve termo-fiziksel özellikleridir. Bu özelliklerin bilgisayar ortamında oluşturulabilmesi için temel gaz denklemlerini ve kullanımlarını, bilgisayar ortamına aktarma yöntemlerini iyi bilerek oluşturmak gerekmektedir.Bu makalede su buharının ve havanın termodinamik özelliklerinin oluşturulması ve bu gazların termodinamik özelliklerinden yola çıkarak su buharı kuru hava karışımı olan nemli havanın özelliklerinin ve yaş hava proseslerinin hesaplanma yöntemlerini inceleyeceğiz. Bu makalede irdelenen nemli havanın termodinamik özellikleri ve yaş hava prosesleri aslında tek başına bir program olmayıp,  çeşitli akışkanların termodinamik ve termo-fiziksel özelliklerinin irdelendiği daha sonra çeşitli proseslerin sayısal irdelenmesi için bir ortam oluşturacak olan bir çalışmanın ilk basamaklarından biridir.  Java dilinde geliştirilen bu ısıl sistem analiz paketi, isteyen tüm araştırıcılarımızın kullanımı için  açık olacaktır.  Nemli havanın termodinamik özelliklerini irdelemek için önce su buharının termodinamik özellikleri ve kuru havanın termodinamik özelliklerinin nasıl hesaplanacağının irdelenmesi gereklidir. Yaş hava (kuru havayı saf gaz kabul edersek), kuru hava ve su buharı karışımından oluşan bir gaz karışımıdır. Bu yüzden önce kuru havanın ve su buharının termodinamik özellikleri irdelenecek  ve daha sonra yaş hava proseslerinin hesaplanması üzerinde durulacaktır.

 

2.Kuru Havanın Termodinamik Özelliklerinin Hesaplanması

Kuru hava termodinamik denklemlerini oluştururken kuru havanın ideal gaz olduğunu kabul edeceğiz. Bu kavram çok düşük sıcaklıklara inmediğimiz durumlar için genelde doğru olarak kabul edilebilir. Çok soğuk uygulamalarına geçildiğinde ise bu kabul doğru değildir, fakat bu sıcaklıklarda su buharının kısmi basıncı neredeyse yok sayılacağından havayı tamamen kuru hava olarak kabul edebiliriz. Kuru hava için bir çok modelde havanın özgül ısısının sabit olduğu kabulü yapılır. Burada havanın özgül ısısının sıcaklığın fonksiyonu olarak değiştiği ancak basınç veya yoğunluğun fonksiyonu olarak değişmediğini varsayacağız(ideal gaz varsayımı).  Ayrıca özgül ısı kısmi devamlı denklemler olarak verilecektir.  Bunun sebebi hava entalpi denkleminin tablolarda verilen denklemlerle daha uyumlu olmasının sağlanmasıdır. Kuru hava özgül ısı denklemi :

 

Cpi(T) = Ai + Bi*10-3*T+ Ci*105/T2+Di*10-6*T2     TLi  >= T   >  THi         KJ/kmol K               (1)

 

Şeklinde tanımlanmıştır. Buradaki Ai, Bi, Ci, ve   Di denklemin TLi  ve THi   sıcaklık bölgesinde geçerli olan denkleminin katsayılarıdır. Çeşitli sıcaklık aralıkları için çeşitli katsayılar tanımlanabilir. Bu katsayılar gerçek tablo değerlerinden eğri uydurma yöntemleri yardımıyla elde edilirler. Eğri uydurmalarda en küçük kareler yöntemi genelde en yaygın olarak kullanılan  yöntemdir. Bu yöntemde ölçümlerden elde edilen değerler ile fonksiyonun aynı noktalarda verdiği değerlerin farkının karelerinin toplam fonksiyonu mininimize edilir. Burada verilen özgül ısı denklemi doğrusal olmayan bir eşitlik olduğundan minimize işleminin de doğrusal olmayan bir teknikle yapılması gerekir. Bu tür denklemlerin çözülmelerinde Nelder-Mead, en dik eğim metodu gibi geometriksel ve genetik algoritmalar gibi geometrik olmayan metotlar mevcuttur. Doğrusal olmayan denklemlerin minimizasyonu oldukça geniş bir konu olduğundan buna daha sonra bir yazımızda değinebiliriz. Hava için

kullanılan katsayılar tablo 1’de verilmiştir.

 

Tablo 1. Hava için özgül ısı kısmi devamlı denkleminin katsayıları

Ai

KJ/kmol K

Bi

103*KJ/(kmolK2)

Ci

10-5*00KJ K/kmol

Di 106*KJ/(kmolK2)

TLi

K

THi

K

29.04716131384

-0.43371335025

-0.00000234324

1.81771922391

298

300

27.20780497541

2.82769845957

0.65953188644

3.73015894390

300

700

23.15288750543

13.57204518133

1.77125763993

-3.86191395226

700

1200

32.62636562076

2.90565403695

-21.59492884110

-0.42617207916

1200

2000

34.28187299595

1.66394564405

-30.46167281155

-0.16319414802

2000

3000

40.90907696143

-0.88928617682

166.78890105869

0.11814251617

3000

6000

 

Bu sayıların elde edilmesinde kullanılan minimizasyon prosesinde Nelder-Mead tekniği kullanılmış ve tablo değerleri özgül ısı denkleminin integrasyonundan oluşan entalpi denkleminden alınmıştır. Entalpi denklemi denklem 2 de verildiği gibidir. Cpi denklemi kısmi devamlı olduğu için toplam entalpi integrasyonun yanında kısmi devamlı bölgelerin entalpilerinin toplamından oluşur.

 

                                                   (2)

bu denklemdeki h0 entalpi sabiti referans değer olarak alınan 298 K noktasındaki entalpi olup değeri h0=8636.3959339 KJ/kmol olarak alınmıştır. Entropi formülü de entalpi formülünden çıkarılabilir.

                     

                                                        

       Şekil 1-Gas1table. java  programı                                                Şekil 2-steamtable. java  programı

                                                           

……………………(3)

 

buradaki s0=49.101193319821995 KJ/kmolK dir. Referans basınç P0=1 bar olarak alınmıştır. Havanın formulü  O 0.419642N 1.561756Ar 0.009301C 0.0003 olarak alınmıştır ve bu formulle havanın moleküler ağırlığını M=28.964197 kg/kmol olarak hesaplar. Entalpi ve entropi değerleri M değeri kullanılarak KJ/kg bazına dönüştürülür.

 

Havanın entalpisinin 6000 K’e kadar varan bir bölge için hesaplanmış olması yaş hava uygulamaları için gereksiz görünebilir. Ancak belirtilen denklemler sadece yaş hava uygulamaları için geliştirilmemiştir, havanın kullanıldığı her yerde geçerlidirler. Hatta sadece hava için değil değişik katsayıların kullanımıyla tüm ideal gazlar için kullanılan denklemlerdir. Bu denklem sisteminin programlaması da çeşitli gazları hesaplayabilecek şekilde oluşturulmuştur. Genel sınıf gaz.java içinde çok sayıda gazın katsayılar matrisini içerir ve gereğinde hesaplar. 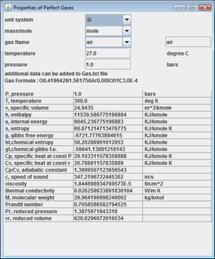“gaz” sınıfı hesaplarının sonuçlarını görebilmek için idealgazTablosu.java isimli bir program geliştirilmiştir ve  bu program kullanılarak hava veya diğer gazların termodinamik özellikleri yukarıda belirtilen denklemler yardımıyla hesaplanabilir. Bu programın çıktısı şekil 1 de gösterilmektedir.

 

3.Su Buharının Termodinamik Özellikleri

Su buharının termodinamik özelliklerinin hesaplanmasında J.H. Keenan, F.G. Keyes , P.G. Hill and J.G. Moore tarafından verilen  [referans 1] denklemler kullanılmıştır.  Su buharı için  yaş havanın bazı hesaplarında ideal gaz kabulü yapılıyorsa da burada su buharı gerçek gaz olarak kabul edilmiştir. Gerçek gazlar genelde hal denklemleri denen ve P(T,v) şeklinde ifade edilebilecek kompleks denklem sistemleriyle ifade edilirler. Burada P basınç. T sıcaklık ve v özgül hacmi ifade etmektedir. Keenan, Keyes,Hill ve Moore denkleminde hal denklemi Helmholtz serbest enerjisi (Y) formunda verilmiştir.

 

                                                 (4)

                                                     (4a)       

    (4b)               

Bu denklemde t=1000/T, T K cinsinden sıcaklık değeridir, R=4.6151 barcm3/gramK  gaz sabitidir. Aij ve Ci  ve E = 4.8 denklem sabitleridir. r yoğunluk değeridir. A sabitinin değerleri Tablo 2 de verilmiştir  taj ve raj tanımları

j=1 için taj= tc=1000/Tc       raj =0.634              (Tc kritik sıcaklık)

j>1 için taj= 2.5                    raj =1.0                   şeklinde verilmiştir.            

 

Tablo 2 : Su buharı Helmholtz serbest enerjisi hal denklemi Y(T,r) katsayıları

Aij 

1

2

3

4

5

6

7

1

29.492937

-5.198586

6.833535

-0.156410

-6.397241

-3.966140

-0.690486

2

-132.139170

7.777918

-26.149751

-0.725461

26.409282

15.453061

2.740742

3

274.646320

-33.301902

65.326396

-9.273429

-47.740374

-29.142470

-5.102807

4

-360.938280

-16.254622

-26.181978

4.312584

56.323130

29.568796

3.963609

5

342.184310

-177.310740

0.000000

0.000000

0.000000

0.000000

0.000000

6

-244.500420

127.487420

0.000000

0.000000

0.000000

0.000000

0.000000

7

155.185350

137.461530

0.000000

0.000000

0.000000

0.000000

0.000000

8

5.972849

155.978360

0.000000

0.000000

0.000000

0.000000

0.000000

9

-410.308480

337.311800

-137.466180

6.787498

136.873170

79.847970

13.041253

10

-416.058600

-209.888660

-733.968480

10.401717

645.818800

399.175700

71.531353

 

Y0(T) denkleminde geçen C katsayıları ise Tablo 3 de verilmiştir.

 

                                               Tablo 3 : Su buharı Helmholtz serbest enerjisi hal denklemi Y(T,r) katsayıları

i

Ci

I

Ci

1

1857.065

5

-20.5516

2

3229.12

6

4.85233

3

-419.465

7

46.0

4

36.6649

8

-1011.249

 

Bu fonksiyonun klasik P(T,v) formülüne göre avantajı termodinamik fonksiyonların sırf türevler cinsinden ifade edilmesidir. P(T,v) formundaki hal denklemleri ise integrallere de gerek duyarlar. Türevlerin hesaplanması integrallere göre daha kolaydır. Türevler cinsinden termodinamik fonksiyonlar şu şekilde tanımlanmıştır:

                                                                        (5a)

                                                                   (5b)

                                                                           (5c)

 h = u +Pv                                                                                (5d)

bu fonksiyonlardaki türev işlemleri açılacak olursa

                                             (6a)

                                                (6b)

                        (6c)

     (6d)

Doymuş su buharı basınç sıcaklık ilişkisi(kaynama eğrisi) aşağıdaki bağıntıyla aynı kaynakta verilmiştir.:

    (7)

Buradaki Fi katsayıları sabittir ve tablo 4 de verilmiştir. Tc and Pc kritik basınç ve sıcaklık değerlerini ifade eder.

 Tablo 4 : su buharı buhar doyma eğrisi katsayıları

i

Fi

i

Fi

i

Fi

i

Fi

1

-741.9242

3

-11.55286

5

0.1094098

7

0.2520658

2

-29.721

4

-0.8685635

6

0.439993

8

0.05218684

Bu denklemleri bilgisayar programlarına adapte ederken bilinmeyen setinin sadece T ve v nin fonksiyonu olmıyacağı da göz önünde bulundurulmalıdır. Örneğin h(T,p) gibi bir bilinmiyen veya denklem 7 kullanılarak T(Ps) doyma noktası sıcaklığı  fonksiyonunun çözümü gibi bir problem karşımıza çıkabilir. Bu tür işlemlerle karşılaştığımızda doğrusal olmayan denklemler, nümerik kök bulma işlemleri karşımıza çıkar. Kök bulma işlemleri taylor formülünden elde edilen yöntemler ve arama yöntemleri veya bunların kombinasyonlarından oluşur. Taylor formülü kökenli yöntemlerden Newton-Raphson metodu bu tür kök bulma algoritmalarının en bilinen yöntemidir. Belli bir tahmin noktasından başlıyarak

formülü kullanır. İterasyon f(x) fonksiyonu isteyen küçüklüğe ulaşıncaya kadar devam eder.Bu formülde xi+1 bilinmiyen kök değeri için (i+1)inci iterasyon, f(xi) fonksiyonun xi noktasındaki değeri, [df(xi)/dx] fonksiyonun xi noktasındaki türevinin değeridir. Bir basit arama metodu olan iki bölge metodu bölgeyi ikiye böler ve kökün hangi bölgede olduğuna bakarak aramaya devam eder. Etkili diğer bir arama kökenli kök bulma yöntemide iki nokta arasında lineer interpolasyonla bir sonraki kök yaklaşımını bulan kiriş yöntemidir. Bunların dışında Secant metodu, Ridder metodu, Van Wijngaarden-Dekker brent metodu gibi çeşitli kök bulma metodları mevcuttur ve bu denklemlerin çözümlerinde yoğun olarak yararlanılmıştır. Tüm bu değişik metodların kullanılması, kök bulmanın kompleks bir işlem olmasından kaynaklanmaktadır, bazı metodlar kısa sürede çözüm getirir ama her zaman çözüme ulaşamaz(newton metodu gibi), bazı metodlarda her zaman çözüme ulaşır fakat iterasyon prosesi çok zaman alır (iki bölge metodu gibi). Bu yüzden belli bir proses için seçilecek metod önem taşır.

Yukarıda tanımlanan temel denklemler kullanılarak su buharının termodinamik özelliklerini hesaplayan steam.java programı geliştirlmiştir. Bu programın kullanıcı arayüzü olarak geliştirilen steamTable.java programı steam.java programını kullanarak buharın termodinamik özelliklerini hesaplamaktadır. Örnek bir program çıktısı  şekil 2’de gösterilmiştir.

4.Yaş havanın Termodinamik Özellikleri

Kuru hava ve su buharının özelliklerinin hesap yöntemlerini inceledik. Şimdi bu programları yaş havanın termodinamik özelliklerini hesaplayacak şekilde bir araya getirelim. Yaş havanın temel termodinamik karışım denklemleri aslında her termodinamik kitabında yer alır ve makine mühendisliği eğitiminde sıkça ısıtma-havalandırma gibi çeşitli derslerinde de kullanılır. Karışım yasalarının temeli iki gazın birlikte bulunduklarında kısmi basınçlarının toplam basıncı oluşturması ilkesine dayanır:

P=Pkuru hava+Psu buharı                                                                                                                                               (8)

Gazların kütlelerinin toplamı da toplam gaz kütlesini oluşturur:

m=mkuru hava+msu buharı                                                                                                                                             (9)

Su buharı kütlesinin kuru hava kütlesine oranı özgül nem olarak adlandırılır:

w = msu buharı / mkuru hava                                                                                      (10)

Özgül nemin değeri bu iki bağıntı ve karışımdaki her iki gazın da ideal gaz olduğu kabulü ile hesaplanabilir. Gazların aynı hacmi işgal ettikleri göz önüne alınırsa:

Pkuru hava V = mkuru hava * (R/Mkuru hava) T                                                            (11a)

Psu buharı V  = msu buharı * (R/Msu buharı ) T                                                             (11b)

Burada P basınç, m kütle, T Kelvin cinsinden sıcaklık değeridir. 8 nolu denklemdeki eşitlikler 7 nolu denklemde yerine konursa

w= {Psu buharı V /[(1/Msu buharı) T]}/ {Pkuru hava /[mkuru hava * (1/Mkuru hava) ]}          (12)                             

w= (Msu buharı/Mkuru hava)   Psu buharı / Pkuru hava = (Msu buharı/Mkuru hava)   Psu buharı / (P - P su buharı )     (13)

bağıntısı elde edilir. Su buharının kısmi basıncı ve toplam basınç biliniyorsa havadaki nem miktarı hesaplanabilir. Denklemdeki molar kütle oranı (Msu buharı/Mkuru hava)=(18.016/28.964197)=0.6220093 sayısına eşittir

Yaş hava hesaplarında kullanılan diğer bir kavram da bağıl nem kavramıdır. Bağıl nem su buharı molar yüzdesinin aynı sıcaklıktaki doymuş su buharı molar yüzdesine oranıdır.

F = xsu buharı/xdoymuş su buharı = Psu buharı/Pdoymuş su buharı                   (14)

Benzer bir kavramda doyma yüzdesidir. su buharı kütlesel yüzdesinin aynı sıcaklıktaki doymuş su buharı kütlesel yüzdesine oranıdır.

m= msu buharı/mdoymuş su buharı = wsu buharı/wdoymuş su buharı                    (15)

Yaş havanın entalpisi de kuru hava ve su buharının entalpilerinden hesaplanır.

H=mkuru hava*hkuru hava + msu buharıhsu buharı                                                                              (16)

H=H/ mkuru hava= hkuru hava + (msu buharı/ mkuru hava )hsu buharı= hkuru hava + w hsu buharı             (16a)

Entropi fonksiyonu da aynı şekilde hesaplanır.

S=mkuru hava*skuru hava + msu buharıssu buharı                                                                               (16)

s=S/ mkuru hava= skuru hava + (msu buharı/ mkuru hava )ssu buharı= skuru hava + w ssu buharı                 (16a)

Yaş hava için kullandığımız diğer bir kavram da adyabatik doyma sıcaklığıdır. Hava sonsuz uzunlukta tamamen izole edilmiş su ile dolu bir kanaldan geçirilirken doyma noktasına ulaşır. Doyma noktasına ulaşmış suyun sıcaklığında yaş havanın sıcaklığına adyabatik doyma sıcaklığı adı verilir. Termodinamik ideal bir kavramdır. Enerji dengesinden hesaplanabilir. Giren havanın enerjisi+ buharlaşan suyun  enerjisi = doymuş havanın enerjisi   olduğundan

h+(w* – w)h*su = h*                                                                                                              (17)

burada h: kanala giren yaş havanın entalpisi, h*: doymuş yaş havanın entalpisi, h*su : kanalda bulunan ve bir kısmı sıvılaşan suyun entalpisi ve w* ise doymuş yaş havanın entalpisidir. Bu denklemin çözümü bize T* adyabatik doyma sıcaklığını verir. Adyabatik doyma sıcaklığı termodinamik yaş termometre sıcaklığı olarak da bilinir. Termodinamik yaş termometre sıcaklığının yaş bir termometrede ölçülen sıcaklıktan farklı olduğunu burada belirtmek gerekir. Gerçek termometrenin okuduğu değer ısı transferine bağlı olarak termodinamik yaş termometre sıcaklığından sapacaktır.

Yaş havayla ilgili tanımlanması gereken son özellikte çiğ noktası sıcaklığıdır. Yaş havanın basıncını değiştirmeden sıcaklığını düşürdüğümüzde aynı basınç altında yoğuşmanın başladığı sıcaklık olarak tanımlıyabiliriz. Verilen kısmi basınç için su buharı yoğuşma sıcaklığına eşittir.

Yukarıda belirtilen denklemler kullanılarak yashava.java programı geliştirilmiştir. Bu program yardımıyla iki termodinamik veri verildiğinde diğer termodinamik değişkenlerin hesaplanması mümkündür. Programda verilebilecek termodinamik veri çiftleri şunlardır :

“tdb_twb"    kuru termometre - yaş termometre sıcaklığı

"tdb_rh"      kuru termometre sıcaklığı - bağıl nem

 "tdb_w"      kuru termometre sıcaklığı - özgül nem

 "tdb_tdew" kuru termometre sıcaklığı - çiğ noktası sıcaklığı

 "tdb_pv"     kuru termometre sıcaklığı - su buharı basıncı

 "tdb_dos"   kuru termometre sıcaklığı – saturasyon derecesi

 "tdb_h"       kuru termometre sıcaklığı - entalpi

 "tdb_s"       kuru termometre sıcaklığı - entropi

 "w_rh"        özgül nem    - bağıl nem

 "w_h"         özgül nem    -  entalpi

Termodinamik veri çiftini seçtikten sonra bu veri değerlerini  girdiğinizde program  termodinamik verilerin değerlerini hesaplayarak verecektir.. Örneğin 25 derece kuru termometre sıcaklığı ve 20 derece yaş termometre sıcaklığı,1.01325 bar basınç için kendi java programımızda yaş havanın özelliklerini hesaplamak için

 

yashava y=new yashava();

double a[]=y.property("tdb_twb",25.0,20.0,1.0132);

 

tanımını girmemiz yeterli olacaktır. Çıktıdaki a vektörüne yaş havanın termodinamik özellikleri yüklenmiş olacaktır. Çıktı vektöründeki değişkenler:

 

a[0]= P, basınç                    

a[1]= T, kuru termometre sıcaklığı 

a[2]= v, kuru hava özgül hacim     

a[3]= Pv su buharı kısmi basıncı   

a[4]= Pa hava kısmi basıncı        

a[5]= w, özgül nem                 

a[6]= rh, bağıl nem                

a[7]= dos, doygunluk derecesi       

 

a[8]= h enthalpi                  

a[9]= s, entropi                   

a[10]= tdew,çiğ noktası sıcaklığı 

a[11]= ha, kuru havanın entalpisi 

a[12]= hv, su buharının entalpisi 

a[13]= hv*w, duyulur enthalpi     

a[14]= T yaş hava sıcaklığı       

 

şeklindedir. Bir çoğumuz için programlama gerekli olmayabilir, sadece bir program kullanarak yaş hava özelliklerinin hesaplanması bizim için yeterli olacaktır. Bu hesaplama sistemi için psT.java programı hazırlanmış arayüzü programı hazırlanmıştır.Programı çağırdığımızda:

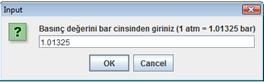
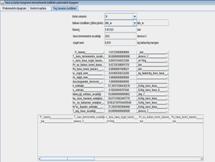
Şekil 3 psT.java programı giriş ekranı

 

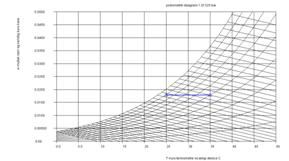
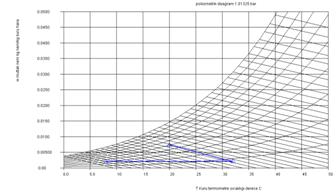
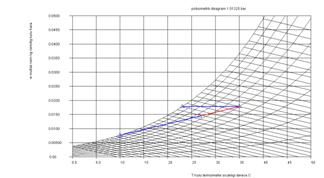
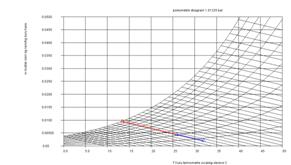
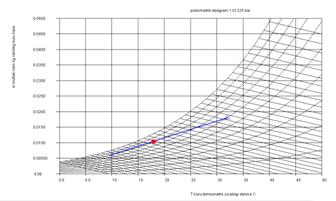
önce basınç değerini girdiğimiz bir ekran belirecektir. Şekil 3 de basınç giriş ekranı görülmektedir. Buradan kullanacağımız basınç değerini girebiliriz. Bundan sonra girdiğimiz basınçta çizilmiş bir psikometrik diyagram karşımıza gelecektir. Bu ekran aktif grafik ekranıdır, yaş hava prosesimizi oluşturmak için istediğimiz kuru termometre sıcaklığı – özgül nem çiftini bu ekran yardımıyla istediğimiz noktada farenin tuşuna basarak girebiliriz. Girdiğimiz noktada bir yıldız belirecektir. Farenin aktif koordinatları ekranın alt köşesinde görebiliriz. Şekil 4 te bu ekran görülmektedir. Girdiğimiz değerler sonucunda hesaplanan termodinamik özellikleri görmek için sayfa üzerindeki yaş havanın özellikleri düğmesine basmamız gerekir. Karşımıza şekil 5 te görülen ekran çıkacaktır. Bu ekranda temel olarak 3 kısım mevcuttur. Birinci kısımda bilinen iki termodinamik veri çiftini seçip değerleri girebildiğimiz bir veri giriş kısmı, en son girdiğimiz verinin sonuçlarının bulunduğu bir tablo ve girdiğimiz tüm verilerin listelendiği kopyalanabilir bir yazım bölümü mevcuttur. Giriş kısmından yeni bir değer girdiğimizde, bu değer ilk psikrometrik diyagram grafik ekranına da yeni bir yıldız olarak çizilecektir. Kopyalanabilir yazım bölümündeki veri yukarıdaki küçük java program örneğindeki a vektörünü açıklarken verdiğimiz sırada verilmiştir. Bu bölümde veri başlıkları da yer almaktadır. Eğer kopyalanabilir yazım bölümündeki tüm veriyi bir text dosyasına aktarmak istersek bu bölümü fare ile işaretleyip Ctrl-C (kopyala) tuşuna basmamız ve yazacağımız text dosyasını açıp Ctrl-V (Yapıştır) komutunu kullanmamız yeterlidir. Veriyi bir text dosyasına kopyaladıktan sonra istendiğinde excel gibi bir programda da açmamız mümkün olacaktır.

Şekil4-PsT.java  programı psikometrik tablo grafik giriş ekranı

Şekil 5 –psT.java  programı tablo veri giriş – tablo veri çıkış ekranı

 

Kontrol sayfasına bastığımızda psikrometrik diyagram grafiğinin kontrol değerlerine ulaşabiliriz. Bu değerler yardımıyla grafiğimizi değişik bir skalada, değişik ekran çizgi sayılarıyla tekrar oluşturabilir, proses detaylarına daha yakından bakabiliriz.

 

5.Yaş Hava Prosesleri:

 

Oturduğumuz veya çalıştığımız bir ortamı istenen sıcaklık ve nemde tutabilmek için iklimlendirme adı verdiğimiz işlemlere gerek duyarız. Bu işlemler duyulur ısıtma(sıcaklığın yükselmesi), duyulur soğutma(sıcaklığın düşürülmesi),  nemlendirme(su buharının eklenmesi),ve nem alma(su buharının havadan ayrılması)’dır. Havayı istenen sıcaklık ve nem düzeyine getirmek için bazı durumlarda bu işlemlerin birkaçı birden uygulanır.

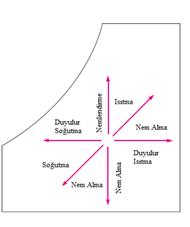
Şekil 6 Yaş hava proseslerinin psikometrik diyagramda tanımlanması

 

Değişik iklimlendirme işlemleri şekil 6’da,Psikrometrik diyagramda gösterilmektedir. Duyulur ısıtma ve duyulur soğutma işlemleri bu diyagramda yatay birer doğru olarak gösterilmektedir,çünkü bu işlemler sırasında havadaki nem miktarı sabittir(w=sabit). Hava kış aylarında ısıtılır ve nemlendirilir, Yaz aylarında ise soğutulur ve nemi alınır.

İklimlendirme işlemleri genellikle sürekli akışlı açık sistemlerde gerçekleşir. Bu nedenle sürekli akışlı açık sistemler için kütlenin (hem kuru hava,hem de su için) ve enerjinin korunumu denklemleri uygulanmalıdır:

Kuru hava kütlesi: ma,g= ma,ç         (18)

Su kütlesi: ma,g wg+ msu,g=  ma,ç wç+ msu,ç       (19)

Enerji: Q-W= mç hç - mg hg           (20)

Burada g ve ç indisleri sırasıyla giriş ve çıkış hallerini ifade etmektedir.Enerji denkleminde kinetik ve potansiyel enerji değişimleri ihmal edilmiştir.

 

a.Duyulur Isıtma ve soğutma:

 

Evlerimizde, işyerlerimizde veya bulunduğumuz ortamlarda soba, radyatör, ısı pompası veya elektrikli ısıtma sistemleri vardır. Bu sistemlerde hava, içinde sıcak bir akışkanın bulunduğu boruların veya direnç tellerinin üzerinden geçirilerek ısıtılır. Bu durum şekil 7’de gösterilmektedir.

                Şekil 7 Yaş havanın ısıtılması

Isıtma işlemi sırasında havadaki nem miktarı değişmez, çünkü nemlendirme veya nem alma söz konusu değildir. Başka bir ifadeyle, nemlendirme veya nem almanın söz konusu olmadığı bir ısıtma veya soğutma işleminde, özgül nem sabit kalır(w=sabit). Bu tür bir ısıtma işlemi, psikrometrik diyagramda yatay bir doğru olarak görünen sabit özgül nem doğrusu üzerinde, artan kuru termometre sıcaklığı yönünde gelişir. Duyulur ısıtma sırasında havanın özgül nemi “w” sabit kalırken bağıl nemi azalmaktadır. Bunun nedeni bağıl nemin havadaki nem miktarının, havada aynı sıcaklıkta bulunabilecek en çok nem miktarına oranı olarak tanımlanması ve havada bulunabilecek nem miktarının sıcaklıkla artmasıdır.

 

Sabit özgül nemde soğutma(duyulur soğutma)yukarıda açıklanan duyulur ısıtma işlemine benzerdir,fakat bu işlem sırasında kuru termometre sıcaklığı azalır ve bağıl nem artar.Duyulur soğutma,havayı içinden soğutucu akışkan veya soğuk su akan boruların üzerinden geçirerek sağlanabilir. Nemlendirme veya nem almanın olmadığı ısıtma veya soğutma işlemlerinde kütlenin korunumu denklemi,kuru hava için

ma,1 =ma,2 =ma  ve su için

w1 =w2

bağıntılarına dönüşür. Fan işi ihmal edilirse, enerjinin korunumu denklemi aşağıdaki biçimi alır:

Q= ma (h2 – h1)  (Kw) veya q= h2 – h1   (kj/kg)  

Burada h2 ve h1  havanın sırasıyla giriş ve çıkışta, birim kuru hava kütlesi için verilen entalpi değerleridir.

Yukarıda verilen bağıntılardan yararlanarak duyulur ısıtma ve duyulur soğutma için  java programlama dilinde program yashavaprosesleri.java programı geliştirilmiştir. Bu programı kullanarak her iki proses için ayrı ayrı vermiş olduğu örnekleri inceleyelim.

Duyulur ısıtma örneğinde,kütleyi 1 kg/s,giriş sıcaklığını 80C,giriş bağıl nem değerini %30 ve çıkış sıcaklığını 320C aldığımızda geliştirdiğimiz java programı ile hesaplamış olduğumuz çıktı değerleri aşağıda verilmektedir:

 

 

 

 

 

 

 

 

 

 

        Şekil 8 Duyulur Isıtma Prosesi Değerlerinin Psikrometrik Diyagramda Gösterilişi

 

Duyulur soğutma örneğinde kütleyi 1 kg/s,giriş sıcaklığını 350C,giriş bağıl nem değerini %50 ve çıkış sıcaklığını 250C aldığımızda geliştirdiğimiz java programı ile hesaplamış olduğumuz çıktı değerleri aşağıda verilmektedir:

 

 Şekil 9 Duyulur Soğutma Prosesi Değerlerinin Psikrometrik Diyagramda Gösterilişi

 

b.Isıtma ve Nemlendirme:

 

Duyulur ısıtmada bağıl nemin azalmasından dolayı ortaya çıkan sorunlar, ısıtılan havayı nemlendirerek yok edebilir.

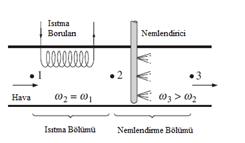
                                Şekil 10

Bu işlem şekil 10’da görüldüğü havayı önce bir ısıtma bölümünden (1-2 hal değişimi) daha sonra da nemlendirme bölümünden (2-3 hal değişimi) geçirerek gerçekleştirilir. 3 hali nemlendirmenin nasıl yapıldığına bağlıdır. Eğer nemlendirme buhar püskürterek gerçekleştirilirse,nemlendirmenin yanında ısıtma da yapılmış olacaktır (T3 > T2). Eğer nemlendirme su püskürterek gerçekleştirilirse,buharlaşma gizli ısısı havadan sağlanacak,bu nedenle hava sıcaklığı azalacaktır (T3 < T2). Bu durumda hava, nemlendirme sırasındaki sıcaklık düşmesini karşılamak için,ısıtma bölümünde daha yüksek bir sıcaklığa ısıtılmalıdır.

Isıtma_nemlendirme prosesini ısıtma_nemlendirme ve ısıtma_adyabatik nemlendirme olarak iki ayrı proseste inceledik.Şimdi bu prosesi geliştirdiğimiz örneklerle inceleyelim. Isıtma_nemlendirme prosesi örneğinde,kütleyi 1 kg/s, T1=80C, f1(bağıl nem)=%30 ,T2=320C, T3=200C, f3=%50 olarak aldığımızda geliştirdiğimiz java programı ile hesaplamış olduğumuz çıktı değerleri aşağıda verilmektedir:

 

Şekil 11 Isıtma_Nemlendirme Prosesi Değerlerinin Psikrometrik Diyagramda Gösterilişi

 

Isıtma_adyabatiknemlendirme prosesi örneğinde,kütleyi 1 kg/s, T1=80C, f1(bağıl nem)=%30, T2=320C, T3=200C, (adyabatik nemlendirmede çıkış bağıl nem değeri%100’dür.) olarak aldığımızda geliştirdiğimiz java programı ile hesaplamış olduğumuz çıktı değerleri aşağıda verilmektedir:

 

Şekil 12 Isıtma_Adyabatiknemlendirme Prosesi Değerlerinin Psikrometrik Diyagramda Gösterilişi

 

c.Soğutma ve Nem Alma:

Duyulur soğutma sırasında havanın özgül nemi sabit kalır, fakat bağıl nemi artar. Eğer bağıl nem istenmeyen ölçüde artarsa, havadaki su buharı miktarını azaltmak,başka bir deyişle nem almak gerekebilir. Bunu gerçekleştirmek için, havanın çiğ noktası sıcaklığından daha düşük bir sıcaklığa soğutulması gerekir.

Nem alma ile birlikte soğutma işleminin nasıl gerçekleştirildiği şekil 13’te gösterilmektedir.

                     

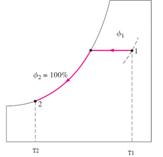
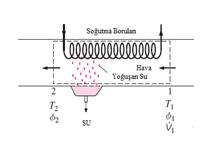
                                                                                   Şekil 13

Ilık ve nemli hava soğutma bölümüne 1 halinde girer.Soğutucu serpantinin üzerinden geçen havanın,sıcaklığı azalır ve özgül nemi sabit kalırken bağıl nemi artar.Eğer soğutma bölümü yeterince uzunsa,hava çiğ noktası sıcaklığına erişir(2 hali,doymuş hava).Havanın daha fazla soğutulması bir miktar su buharının yoğuşmasına neden olur.Yoğuşma devam ederken havanın hali,doymuş hava eğrisi (%100 bağıl nem eğrisi)üzerinde ilerleyerek son hale ulaşır(3 hali).Soğutma ve nem alma işlemleri birlikte ele alınırsa ,kütlenin ve enerjinin korunumu denklemleri aşağıdaki biçime dönüşür:

Kuru hava kütlesi:  ma1= ma2= ma

Su kütlesi: ma1 w1 = ma2 w2 + msu   veya msu = ma (w1- w2)

W=0 olduğu için Q=Ʃ mç hç -Ʃ mg hg       Q= ma (h2- h1)+ msu hsu

Bu denklemlerden yararlanarak  geliştirdiğimiz java programı ile soğutma_nemalma_ısıtma prosesi ve soğutma_nemalma_karıştırma prosesi için iki ayrı örnek verilmiştir:

Soğutma_nemalma_ısıtma prosesi örneğinde,kütleyi 1 kg/s, T1=320C, f1(bağıl nem)=%70, T2=220C, f2=%45 olarak aldığımızda geliştirdiğimiz java programı ile hesaplamış olduğumuz çıktı değerleri aşağıda verilmektedir:

 

 

Şekil 14 Soğutma_nemalma_ısıtma Prosesi Değerlerinin Psikrometrik Diyagramda Gösterilişi

 

Soğutma_nemalma_karıştırma prosesi örneğinde,m1= 1 kg/s, T1=350C, f1(bağıl nem)=%50, T2=100C, m2=0.5kg olarak aldığımızda geliştirdiğimiz java programı ile hesaplamış olduğumuz çıktı değerleri aşağıda verilmektedir:

 

Şekil 15 Soğutma_nemalma_karıştırma Prosesi Değerlerinin Psikrometrik Diyagramda Gösterilişi

 

d.Evaporatif(Buharlaştırmalı)Soğutma:

Günümüzde iklimlendirme sistemlerinin çalışma ilkesi soğutma çevrimine dayanır.Bu sistemler her yerde kullanılabilirler,fakat ilk yatırım ve işletme giderleri yüksektir.Çok sıcak ve kuru yerlerde iklimlendirmenin yüksek maliyeti buharlaştırmalı soğutucular kullanılarak önlenebilir. Evaporatif (buharlaştırmalı) soğutma basit bir ilkeye dayanır:Su buharlaşırken buharlaşma gizli ısısı su kütlesinden ve çevre havadan sağlanır.Bunun sonucu olarak hem su hem de hava soğur.Bu yöntem yüzyıllardan beri içme suyunu soğutmak için kullanılmıştır. Sıcak,kuru bir günde avlunun sulandığı zaman daha serin olduğu dikkatinizi çekmiştir.Bunun nedeni suyun buharlaşırken çevreden ısı almasıdır.Evaporatif (buharlaştırmalı) soğutucu da aynı ilkeye göre çalışır.Evaporatif (buharlaştırmalı) soğutma sistemi şekil 16’da açıklanmıştır.

                     

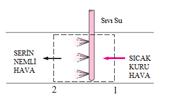
                                                                         Şekil 16

 

Sıcak ve kuru hava buharlaşmalı soğutucuya 1 halinde girer ve burada içine su püskürtülür.İşlem sırasında suyun bir bölümü hava akımından ısı çekerek buharlaşır.Bunun sonucu olarak hava akımının sıcaklığı azalır ve nem miktarı artar(2 hali).Hava bu işlemle en çok 2’ haline soğutulabilir.2’ halinde hava doymuş olup,erişebileceği en düşük sıcaklığa erişmiştir.

Evaporatif (buharlaştırmalı) soğutma işlemi,adyabatik doyma işlemiyle hemen hemen aynıdır,çünkü hava akışıyla çevre arasındaki ısı geçişi genellikle ihmal edilebilir.Bu nedenle,buharlaştırmalı soğutma işlemi psikrometrik diyagramda sabit yaş termometre sıcaklığı doğrusunu izler.Su sıcaklığının havanın son haldeki sıcaklığından farklı olması durumunda,bunun tam olarak böyle gerçekleşmeyeceği not edilmelidir.Sabit yaş termometre sıcaklığı doğrularıyla sabit entalpi doğruları hemen hemen çakıştığı için,akış sırasında havanın entalpisinin değişmediği kabul edilebilir.Başka bir deyişle,evaporatif (buharlaştırmalı) soğutma sırasında,

Tyt=Sabit     (21)

 h=Sabit       (22)

olur.Bu bağıntılar oldukça hassas sonuçlar verir ve iklimlendirme hesaplarında yaygın olarak kullanılmaktadır.

Evaporatif (buharlaştırmalı) soğutmayı bir örnekle pekiştirelim: m1= 1 kg/s, T1=320C, f1(bağıl nem)=%6, T2=260C olarak aldığımızda geliştirdiğimiz java programı ile hesaplamış olduğumuz çıktı değerleri aşağıda verilmektedir:

Not:Evaporatif (buharlaştırmalı) Soğutma prosesi adyabatik soğutma işlemiyle aynı olduğu için program adyabatik soğutma prosesi programı olarak geliştirilmiştir.

 

Şekil 17 Evaporatif(buharlaştırmalı) Soğutma Prosesi Değerlerinin Psikrometrik Diyagramda Gösterilişi

 

e.Hava Akışlarının Adyabatik Olarak Karıştırılması:

 

İklimlendirme uygulamalarının çoğunda iki hava akışının karıştırılması gerekir.Bu durum özellikle büyük binalarda,fabrika,imalat atölyeleri ve hastanelerde kullanılmaktadır.Bu gibi yerlerde iç havanın istenen koşullara getirilmesinden sonra,temiz dış havayla karıştırılarak odalara veya çalışma yerlerine gönderilmesi gerekir.Karıştırma işlemi şekil 18’de gösterildiği gibi iki hava akışını birleştirerek sağlanır.

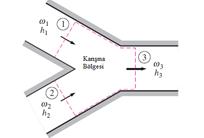
                                                        Şekil 18

 

Karıştırma işlemi sırasında çevreye olan ısı geçişi genellikle azdır,bu nedenle işlem adyabatik kabul edilir.Karıştırma işlemi sırasında iş etkileşimi yoktur,kinetik ve potansiyel enerji değişimleri de ihmal edilebilir.Bu kabullerle,iki hava akışının adyabatik olarak karıştırılması sırasında kütlenin ve enerjinin korunumu denklemleri aşağıdaki gibi olur:

Kuru hava kütlesi: ma3 = ma2  + ma1         (23)

Su buharı kütlesi:  ma1 w1 + ma2 w2 = ma3 w3      (24)

Enerjinin korunumu:   ma1 h1 + ma2 h2 = ma3 h3   (25)

Bu denklemlerden ma3  yok edilirse,

  ma1 /ma2  =  ( w2 -  w3)/(  w3 -  w1 ) = ( h2- h3 )/( h3 - h1)    (26)

bulunur.Bu denklemin psikrometrik diyagramda geometrik bir yorumu yapılabilir.Denklem,

( w2 -  w3)/(  w3 -  w1) oranının ( ma1 /  ma2) oranına eşit olduğunu belirtmektedir.Bu koşulu sağlayan haller şekil 19’da AB kesik doğrusuyla gösterilmiştir. ( h2- h3 )/( h3 - h1)  oranı da ma1 /ma2  oranına eşittir.Bu koşulu sağlayan haller de şekil 18’de CD kesik doğrusuyla gösterilmiştir.Her iki koşulu sağlayan hal ise bu iki doğrunun kesişim noktasıdır ve 1 ve 2 hallerini birleştiren doğru üzerindedir.Buradan şu sonuçları çıkarmak mümkündür:Farklı hallerdeki iki hava akışı (1 ve 2 halleri) adyabatik olarak karıştırıldığı zaman,karışımın hali(3 hali),psikrometrik diyagramda 1 ve 2 hallerini birleştiren doğru üzerinde olur;2-3 uzunluğunun 3-1 uzunluğuna oranı ise,kütle debilerinin oranı  ma1 /ma2  oranına eşittir.

Doyma eğrisinin iç bükey olması ve yukarıdaki sonuç ilginç bir olasılığı belirtmektedir.1 ve 2 halleri doyma eğrisinin yakınında olduklarında,bu iki hali birleştiren doğru doyma eğrisini kesecek ve 3 hali doyma eğrisinin solunda kalabilecektir.Bu durumda bir miktar su buharı yoğuşur.

Karıştırma prosesini kütlesel karışım ve hacimsel karışım olarak iki ayrı örnekle inceledik.

Kütlesel karışım örneğinde ; m1= 183 kg/s, T1=100C, f1=%80, m2=111kg/s,T2=320C,f2=%60 olarak aldığımızda geliştirdiğimiz java programı ile hesaplamış olduğumuz çıktı değerleri aşağıda verilmektedir:

 

Şekil 19 Kütlesel Karışım Prosesi Değerlerinin Psikrometrik Diyagramda Gösterilişi

 

Hacimsel karışım örneğinde ; m1= 183 m3/h, T1=100C, f1=%80,m2=111m3/h,T2=320C,f2=%60 olarak aldığımızda geliştirdiğimiz java programı ile hesaplamış olduğumuz çıktı değerleri aşağıda verilmektedir:

 

 

Şekil 20 Hacimsel Karışım Prosesi Değerlerinin Psikrometrik Diyagramda Gösterilişi

 

Sonuçlar:

 

Bu çalışmada, kuru hava ve su buharının termodinamik özelliklerinin tanımlanması ve bu özelliklerin hesaplanması, ayrıca yaş hava proseslerinin temel özellikleri ve bu proseslerin hesaplanması hakkında bilgi verilmiştir.Bu proseslerin  hesaplanması için java programlama dilinde  bir program geliştirdik ve yaş hava proseslerinin hesaplanmasında bu geliştirmiş olduğumuz program sayesinde, iklimlendirme uygulamalarında karşımıza çıkacak olan problemlerin çözümünde  biz mühendisler için   faydalı bir kaynak olacağına inanıyorum.

 

Kaynaklar:

1.Yunus Çengel, Michael Thermodynamics An Engineering Approach,5th ed.,McGraw-Hill-Chapter 14.

2.Air  Conditioning and Refrigeration Mechanical Engineering Handbook.

3.Handbook of Air Conditioning and Refrigeration-Shan K.Wang.

4. Keenan, J; Keyes, F.G; Hill, P.G.; Moore, J.G., Steam Tables, Thermodynamic Properties of Water Including Vapor, Liquid and Solid, Willey Interscience publication, 1969, ISBN 0-471-04210-2

5. M. Turhan Çoban, Java 2 Programlama Kılavuzu, ALFA yayınevi, ticarethane sok no 41/1 34410 cagaloglu Istanbul, ISBN 975-316-631-1

6.  M. Turhan Çoban, Sayısal Metodların Soğutma Dünyasına uygulanması : Yaş havanın Termodinamik özellikleri, Soğutma Dünyası ISSN 1304-1908 Ekim-Aralık 2006